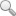閱讀 3798 次 條形荷載下加筋土邊坡破壞機制的數值模擬
條形荷載下加筋土邊坡破壞機制的數值模擬
高文華 RichardJ Bathurst
湖南科技大學 湖南湘潭411201 加拿大皇家軍事學院(RMC) 金斯敦安大略省 ON K7K 784
引言
對于加筋土邊坡的穩定性分析,目前一般采用整體圓弧滑動法或Bishop及Janbu條分法,并計入筋材抗拉強度的影響。其滑動面形狀假定為圓弧形破裂或對數螺線形破裂或直線型破裂。但這是基于均質、各向同性的黏性土坡的穩定性分析一種簡化方法。
對于條形荷載作用下加筋土邊坡的破壞機制,Chungsik Yoo曾做過一系列的小型室內模型試驗。模型尺寸為1.7m(長)×0.5m(寬)×0.6m(高),坡度為34°。條形荷載寬80mm,距坡肩l20mm。填土材料采用細砂,并采用3層高強度的雙向土工格柵。試驗結果表明,邊坡的破裂面為非圓弧形。
為了克服模型的尺寸效用,獲得加筋與不加筋邊坡在條形荷載下的各種性狀參數和邊坡的破壞機制,Richard J.Bathurst曾在加拿大皇加軍事學院(RMC)做過3個大型的室內足尺試驗,對邊坡內部土的位移、土工格柵的應變和位移、條形基礎(鋼梁)施加的荷載和位移等進行了詳細的觀測和記錄,獲得了加筋邊坡在條形荷載下的極限承載能力和邊坡雙楔體的破壞模式,并采用極限平衡法對邊坡的極限承載能力進行了分析。本文擬以此試驗為基礎,采用基于有限差分的連續介質快速拉格朗日分析方法(FLAC),對條形荷載作用下加筋土與非加筋土邊坡的破壞機制及其影響因素進行數值模擬和分析。
1、數值模擬
1.1數值計算模型
RMC在室內共進行了3個試驗。加筋土邊坡試驗剖面如圖1所示,一個是未加固的邊坡,另外兩個分別采用剛度和強度差別較大的4層土工格柵加固。3個試驗模型的幾何尺寸和土的性質完全相同。試驗用砂取于當地,級配較差。加載前土的平均密度為18.1kN/m,。在低圍壓下的峰值摩擦角為60°,高圍壓下為50°,最佳擬合值為53°,體積摩擦角為38°,剪脹角為l50°土工格柵的垂直間距為0.75m,距離模型基礎的高程分別為0.63m,1.38m,2.13m,2.88m。土工格柵一直鋪設到模型后部,以免被直接拉出而破壞。模型頂部布置了加載系統,可以通過液壓激勵器施加l000kN的垂直條形荷載。加載寬度和位置見圖1。為了記錄在試驗過程中邊坡的反應,對下列項目進行了測試:①邊坡坡面的水平和垂直位移;②條形加載鋼梁前后土的垂直位移;③邊坡內部土的位移;④垂直土壓力和一些特定點的水平土壓力;⑤土工格柵的應變和位移;⑥條形基礎(鋼梁)施加的荷載和位移;⑦土的溫度。
3個模型均采用增量加載直至模型破壞為止。模型1~模型3的破壞荷載分別為400kN,650kN和840kN。根據儀器測試和模型拆卸開挖揭示的情況,呈現出明顯的雙塊楔體破壞模式(圖1)。
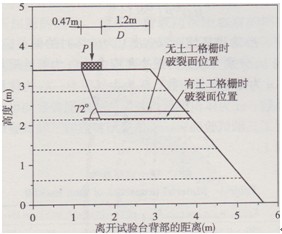
圖1邊坡剖面及破壞面位置
數值計算工作在加拿大皇家軍事學院巖土工程研究中心進行,數值分析采用美國Itasca工程咨詢公司開發的基于有限差分分析的FLAC2D Version5.0軟件。分析中將邊坡簡化為平面應變問題,土體采用均勻、各向同性的非線性彈塑性材料模擬,并采用考慮剪脹效應的Mohr—Coulomb屈服準則,采用不相適應的流動法則。土工格柵采用錨索結構單元進行模擬。邊坡的頂部和坡面為自由邊界;邊坡的底部為剛性基礎,可視為固定邊界;邊坡背部錨固在基礎之上的豎向預應力混凝土模板對坡體的約束可視為鉸支,即在水平方向無位移,在豎直方向無約束。為了適用邊坡在加載至破壞過程中出現的大位移反應,采用大變形模式進行模擬。圖2為計算模型簡圖。

圖2有限差分網格劃分
1.2土體材料本構模型及其參數
土體的非線性彈性響應采用Duncan—Chan9雙曲線模型E—B模式加以描述,其切線變形模量El和、體積模量B可分別表達為:式中:Rf為破壞比;(σ1-σ3,),為破壞時的偏差應力;σ1與σ3,分別為最大與最小主應力;Ke為彈性模量系數;n為彈性模量指數;Pa為大氣壓力;Kb為體積模量系數;m為體積模量指數。這些模型參數均可由常規土工三軸試驗確定。
1.3土工格柵本構模型及其參數
邊坡2采用的土工格柵為聚丙烯(PP),其剛度和強度相對較弱;邊坡3采用的為高強聚乙烯(HDPE),其剛度和強度比PP要強得多。材料的性質和參數見表2,數據是按照美國材料與試驗學會(ASTM l996)D4595—96號實驗標準試驗獲得的。
土工格柵采用兩節點的彈塑性錨索結構單元進行模擬。該單元只能受拉,不能受壓。
1.4筋土接觸面特性
為了反映在條形荷載下邊坡土體與筋帶之間產生的滑動,采用無厚度的彈簧一滑動系統來模擬筋土之間的相互作用和相對運動。接觸面參數可由直剪試驗和抗拔試驗確定。依據Richard J.Bathurst等人的試驗結果,參數取值如下:接觸面摩擦角Sfriction=50°,接觸面黏聚力或固有剪切強度Sb0d=0kN/m²,接觸面剪切剛度Kbond=l kNm-1m-1。
2、計算結果及其分析
2.1條基荷載與位移響應
為了模擬逐步加載過程,并保持數值計算過程的穩定性,在坡頂相應位置逐步施加一向下的速度向量。從圖3可以看出,隨著荷載增加,位移增大。邊坡極限承載力的計算值分別為246,422,520 kPa,反映出經過格柵加固的邊坡承載能力明顯提高,且隨著格柵剛度和強度的增大而增大。表3為邊坡極限承載力計算值與實測值的對比,計算值與實測值之比分別達95.4%,l00.6%和95.9%。
圖3條形荷載下位移響應的實測值與計算值對比
2.2破壞面的位置與形態
為了確定條形荷載作用下加筋與不加筋邊坡破壞面的位置和形態,分別對3個邊坡的節點位移速度向量、塑性區和剪應變速率分布進行了計算,它們均與破壞面的位置和形態密切相關。
2.3條基荷載位置對破裂機制的影響
為了分析條形荷載位置對破裂機制的影響,取條形荷載距坡肩的距離分別為0.8m、1.2m、1.6m³種不同的荷載位置進行計算。對于加筋和不加筋的邊坡,當條形荷載邊緣距坡肩的距離D由1.2m"0.8m時,邊坡破壞面形態由雙楔體形過渡到圓弧形。這是由于當條形荷載靠近坡頂時σ3將減小。故在同樣的條形荷載作用下,土體的抗剪強度降低,從而在筋帶屈服和筋帶與土體之間產生充分的滑動之前,邊坡土體已經產生了屈服。因此,其破裂面形態與均質土坡的破壞形式相似。而由l.2m"1.6m時,仍為楔體破壞,但楔體的底部的破壞位置加深,這是由于當條形荷載位置遠離坡肩時σ3,增加導致土體的抗剪強度增加的緣故。其原理與條形荷載位置距坡肩l.2m的情形類似。
2.4填土材料強度對破裂機制的影響
為了分析填土強度對破壞機制的影響,選取低塑性黏土為填料,土性參數如下:摩擦角為24°,黏聚力6 kPa,剪脹角為0°,抗拉強度為0kN/m²,土的平均密度為l8.1kN/m,,其他參數不變。無論加筋與不加筋邊坡,其臨界破裂面更接近圓弧形或對數螺線形。這是因為當填土材料強度降低時,特別是土體的摩擦角I;D降低時,土體的屈服應力顯著降低。因此,在條形荷載下,盡管筋帶與土體之間可能產生一定的滑動,但這種滑動還沒有充分產生之前,邊坡土體已經產生了屈服。因此,對于填土材料強度較低的加筋邊坡,其破裂面形態仍可采用均質土坡的破壞形式。
3、結語
(1)數值模擬表明,在距離邊坡坡肩l.2m處施加條形荷載時,邊坡的節點位移速度向量、塑性區和剪應變速率分布均明顯一致地表現出邊坡為折線型雙楔體滑動形態,與圓弧形和直線形臨界滑動面形態明顯不符。滑動楔體的底部近于水平,并位于第二層筋帶和第三層筋帶之間,比實際滑動楔體的底部略低。滑動楔體的側面基本上條形荷載的后部位置一致。與實際觀測到的情況基本吻合。反映出以無黏聚力的粗粒砂土為填料的加筋與不加筋邊坡,在距坡肩l.2m處施加條形荷載時,更適合采用雙楔體破壞模式對邊坡進行分析。
(2)條形荷載位置與破壞面形態密切相關。條形荷載邊緣距離坡肩的位置由l.2m"1.8m時,邊坡破壞面形態由雙楔體形過渡到圓弧形,而由1.2m"1.6m時,仍為楔體破壞,但楔體的底部的破壞位置加深。對于PP和HDPE加固的情況,楔體底部的破壞位置由第三層筋帶附近下移到第二層筋帶位置附近。
(3)無論加筋與不加筋邊坡,當填土材料強度降低時,如低塑性黏土,破裂面形態轉化為圓弧形或對數螺線形。但摩擦角、黏聚力和剪脹角的變化對破裂面的形態的影響規律還有待進一步研究。
(本文來源:陜西省土木建筑學會 文徑網絡:溫紅娟 劉紅娟 尹維維 編輯 文徑 審核)
| 上一篇: 預應力錨索錨固段應力分布影響因素分析 |
| 下一篇: 特大跨徑懸索橋上部結構施工關鍵技術研究 |

 聯系我們...
聯系我們...  圓弧車道施工時標高控制的等分直...
圓弧車道施工時標高控制的等分直...  新技術IDITI 法濕陷性黃土地基處...
新技術IDITI 法濕陷性黃土地基處...  漢長安城遺址保護區安置及開發住...
漢長安城遺址保護區安置及開發住...  高校基礎設施建設BOT項目研究...
高校基礎設施建設BOT項目研究...  陜西土木建筑網簡介...
陜西土木建筑網簡介...  級配壓實砂石墊層在西安地區的施...
級配壓實砂石墊層在西安地區的施...  低碳城市建設在西安的探索與實踐...
低碳城市建設在西安的探索與實踐...  淺談中國古代建筑材料與建筑的發...
淺談中國古代建筑材料與建筑的發...  漢長安城遺址保護區內安置及開發...
漢長安城遺址保護區內安置及開發...  柴油發電機房的火災危險性類別分...
柴油發電機房的火災危險性類別分...  陜西重型機械廠改造規劃設計...
陜西重型機械廠改造規劃設計...  世界十位著名建筑師介紹及其作品...
世界十位著名建筑師介紹及其作品...  西安紡織城藝術區改造設計(一)...
西安紡織城藝術區改造設計(一)...  寶雞市青少年科技活動中心設計...
寶雞市青少年科技活動中心設計...