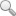密肋復合墻體壓彎剪復合受力性能非線性數值分析

王愛民 姚謙峰 吳敏哲 黃煒

長春工程學院，吉林長春l30012 西安建筑科技大學 陜西西安710055

引言

    密肋壁板結構由于其特殊的構造特點，其受力特性既不同于混凝土框架填充墻結構，也不同于混凝土剪力墻結構，為探討該結構體系的受力特性、破壞模式及抗震性能等，近幾年來，課題組做了大量的試驗及理論研究，尤其對以水平荷載作用為主的小剪跨比密肋復合墻體的受力特性及抗震性能等進行了細致的試驗及理論研究，為該類墻體的受剪承載力計算理論與設計方法的建立及該結構體系在工程中的應用提供了理論依據(該研究成果在文獻[4]中體現)。由于對較大剪跨比密肋復合墻體的試驗及理論研究較少，對該類墻體的破壞模式及特征、承載力的影響因素等認識不足，使復合墻體正截面承載力計算理論及設計方法的建立缺乏依據(文獻[4]中在此方面仍為空白)，影響了密肋壁板結構體系在中高層結構中的應用。本文在密肋復合墻體壓彎剪復合受力性能試驗研究成果[5]的基礎上，應用ANSYS有限元程序，對較大剪跨比密肋復合墻體在壓彎剪復合受力狀態下的破壞形態及特征、承載力、截面正應力及應變特征等受力性能及其主要影響因素進行了數值分析，進一步對試驗研究結果進行擴展，為正確認識密肋復合墻體壓彎剪復合受力機理提供了更多及更為詳實的數據信息，為密肋復合墻體壓彎承載力計算方法及構造措施建立提供了依據。

1、復合墻體非線性有限元計算模型及其驗證

    1.1計算模型

    采用“實體單元一組合式配筋”模型，即混凝土和砌塊采用Solid65的規則六面體單元，柱中縱向鋼筋采用空間桿單元Link8，并且和混凝土單元共用節點，以保證二者變形協調。

    1.2基本假定

    (1)墻體模型簡化為平面應力狀態；

    (2)不考慮縱向鋼筋與混凝土之間的滑移，并忽略箍筋的作用；

    (3)墻板四周與邊框固結，墻體底部固結。

    1.3材料模式

    混凝土提供的單軸受壓狀態下的應力一應變關系。采用William—Warnke五參數破壞準則作為混凝土強度準則。鋼筋采用各向同性理想彈塑性模型(二折線模型)，其強化段的切線模量采用彈性模量的0.01倍。加氣混凝土填充砌塊的力學性能與普通混凝土相似，單軸荷載作用下砌塊的本構關系采用式(1)。同時采用與混凝土相同的破壞準則分析砌塊的彈塑性行為。材料的主要計算參數分別由其強度實測值確定。

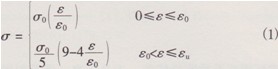
    式中：σo=0.8fqk;εo=0.002；。εu=0.0035。其中，fqk為加氣混凝土砌塊抗壓強度值。

    1.4求解策略與收斂準則

    對增量方程的平衡迭代采用牛頓一拉普森法。為保證容易收斂不考慮混凝土的壓碎作用。為模擬混凝土開裂后應力軟化和混凝土壓碎后的單元負剛度問題，采用自適應下降方法。本文采用力的收斂準則，求解的誤差極限設為5.0×10-2。

    1.5有限元計算模型的驗證

    1.5.1分析對象、有限元計算模型及荷載

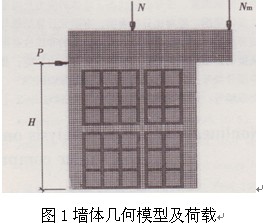
    墻體模型的幾何尺寸及加載模式完全與文獻[5]第4章所述的試驗墻體相同。荷載施加順序為：先施加作用于墻體頂部中心的豎向荷載Ⅳ到最大值(950kN)，然后逐級同步施加作用于墻體頂部的水平荷載P及加載梁端部的豎向偏心荷載Nmo同時，為保證墻體中心的豎向荷載值不變，在此處施加數值等于Nm的反向豎向荷載。試件有限元幾何模型及施加的荷載見圖1示。

    1.5.2有限元計算結果與試驗結果的對比分析

    表1、圖2及圖3分別為2個試件的極限荷載和極限水平側移、二層頂部水平荷載一位移曲線及試件MLQT-Ml在不同加載時刻各柱鋼筋應變分布的有限元結果與試驗值的對比。由表及圖中可得出：

表1有限元計算結果與試驗結果對比

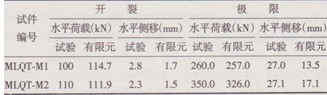
    (1)二層頂部水平位移有限元結果較試驗結果偏小，這主要是因為有限元模型中未考慮砌塊與混凝土框格、復合墻板與邊框架之間的微裂縫以及砌塊之問的拚縫處理，也未考慮復合墻板底部在坐漿層處的滑移。

    (2)墻體中受拉區肋柱鋼筋應變有限元結果略大于試驗結果，這主要是因為有限元模型中未考慮墻板沿豎向的非連續性及非整體性，過高估計了墻體中肋柱對墻體整體受彎的貢獻。

    (3)墻體受壓區鋼筋應變及墻體的受壓區高度有限元計算結果與試驗結果吻合較好。

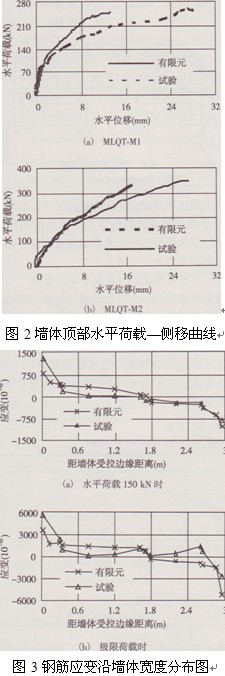
    總之，采用上述有限元模型除對墻體水平側移的估計偏小及對受拉區肋柱鋼筋應變估計稍偏大之外，在墻體承載力、邊框柱鋼筋應變及受壓區高度的模擬中基本具有較好的精確度。考慮到肋柱對復合墻體受彎貢獻不大[5]，因此，以該有限元模型分析復合墻體正截面受彎的受力特性是可行的且可滿足工程精度要求的。

2、復合墻體壓彎剪復合受力性能非線性有限元分析

    2.1分析對象及加載模式

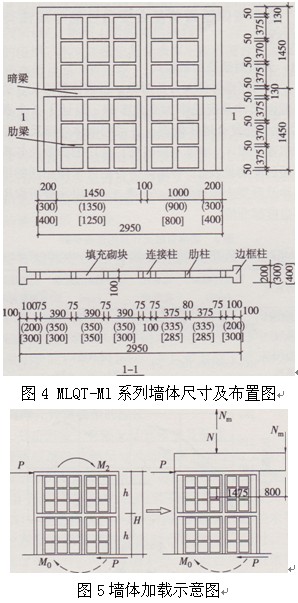
    以兩層墻體作為分析對象，以墻體剪跨比、邊框柱截面尺寸及配筋率為變化參數，設計了3個系列1/2比例的復合墻體模型。各系列墻體外型尺寸及平面布置見圖4，墻體系列名稱、選用的參數及各構件截面和配筋見表2；各墻體中各構件采用相同的鋼筋品種及混凝土強度等級(見表3，有限元分析取用材料強度標準值)。

表2墻體有限元計算的主要參數

    為考慮剪跨比的影響，對不同層數墻體按照保證底部截面所受內力相等原則將全部荷載作用于二層頂部，其中水平彎矩用作用于墻體中心及加載梁端部的一對豎向荷載來模擬，墻體加載示意圖見圖5，墻體頂部作用的水平荷載、彎矩及豎向偏心荷載之間的關系列于表4。墻體荷載施加順序及方法同上所述，作用于墻體中心部位的豎向荷載Ⅳ最大值為950kN。

表4墻體施加荷載之間關系

    注：表中p及H意義見圖1所示

    2.2數值計算結果及其分析

    2.2.1墻體承載力

    表5為各系列墻體極限荷載匯總表。由表中數值可對復合墻體承載力的主要影響因素分析如下：

    (1)剪跨比的影響

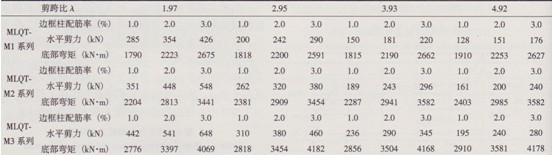
    當墻體邊框柱截面尺寸及配筋率相同時，極限剪力隨剪跨比的增大而減小，但極限彎矩隨剪跨比的增大變化幅度很小。3個系列4個剪跨比墻體的極限剪力平均相差約25％，而極限彎矩最大相差約2％。可見，所有墻體模型的破壞均為正截面彎曲破壞，墻體的受彎承載力對墻體的極限承載力起控制作用。因此，進行較大剪跨比密肋復合墻體截面設計時，必須進行正截面受彎承載力計算。

    (2)邊框柱截面尺寸及配筋率的影響

    當剪跨比相同時，復合墻體的極限荷載隨墻體邊框柱配筋率的增大而增大。但隨剪跨比的增大，邊框柱配筋率的增大對極限荷載的提高幅度降低，尤其當邊框柱截面較小時。反映出當邊框柱截面尺寸較小或配筋率較大時，墻體的彎曲破壞是由受壓側邊框柱混凝土先壓碎造成。因此，當邊框柱截面尺寸較小時，單純提高邊框柱配筋率并不能有效提高復合墻體的受彎承載力。

表5墻體極限荷載有限元計算結果匯總表

    2.2.2墻體彎曲正應力及應變特征

    墻體彎曲正應力及應變特征反映墻體在水平荷載作用下的彎曲受力特性及邊框柱與復合墻板受彎協同工作性能。極限狀態時的應力及應變特征是建立墻體彎曲正截面承載力計算公式的主要依據。圖6及圖7分別為部分墻體底部截面根據各柱鋼筋正應變繪出的截面應變分布圖及混凝土與砌塊正應力分布圖。由圖可總結墻體彎曲應變與應力特征如下：

    (1)隨剪跨比的增大，兩側邊框柱鋼筋應變較連

    接柱及肋柱應變數值明顯增大。但剪跨比的影響隨水平荷載的增大逐漸減弱，當達到極限狀態時，不同剪跨比墻體截面應變數值十分接近，尤其在受壓區應變分布幾乎一致，表明4種不同剪跨比的墻體均為受壓側邊框柱彎曲受壓破壞。

    (2)墻體兩側邊框柱截面內應變以及受壓側邊框柱截面內應力明顯大于其他構件截面內應變及應力，表明墻體整體彎曲作用的影響主要集中在兩側邊框柱內，墻板與邊框柱具有一定的協同受彎性能，但邊框生承擔了大部分整體彎矩，連接柱、肋柱及填充砌塊對墻體整體受彎貢獻不大。

    (3)墻體在壓彎極限狀態時的截面應變呈倒“S”形分布，從嚴格意義上講已不符合平截面假定。但從圖6及圖7中可以發現，墻體兩側邊框柱外邊緣的正應變基本滿足平截面假定，若只考慮兩側邊框柱承擔全部整體彎矩，為便于工程實際應用，在一定精度范圍內，可近似認為墻體在極限狀態時符合平截面假定。

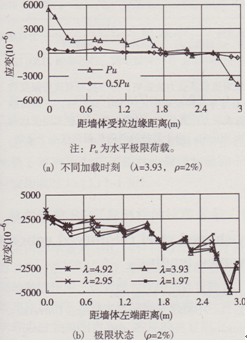
圖6 MLQT-M2系列墻體截面正應變分布

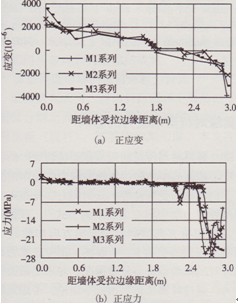
圖7各墻體(p=2％，A=4．92)極限狀態時截面正應變及應力分布

   (4)墻體達到壓彎極限狀態時，兩側邊框柱腹板鋼筋均未屈服。

    2.2.3墻體的彎曲破壞形態及特征

    總結墻體破壞時邊框柱鋼筋應力應變特征，將墻體的彎曲破壞形態分為大偏心受壓破壞(破壞時受拉側邊框柱鋼筋先屈服，受壓側邊框柱混凝土后壓碎及受壓鋼筋屈服)和小偏心受壓破壞(破壞時受壓側邊框柱混凝土壓碎及受壓鋼筋屈服，而受拉側邊框柱鋼筋未屈服)兩種。由于小偏心受壓破壞時，復合墻體受拉側邊框柱鋼筋未屈服，受壓側邊緣混凝土極限壓應變較大偏心受壓破壞的墻體明顯偏小，反映出墻體的破壞為脆性破壞，設計時應予以避免。表6列出了發生兩種破壞形態的墻體系列編號及其主要參數，從中可知：

表6墻體破壞形態匯總表

    注：大為大偏壓破壞；小為小偏壓破壞。

    (1)剪跨比較小的墻體(λ=2.95)均發生大偏心受壓破壞，而剪跨比較大的墻體(λ=4.92)，在其他條件相同時，由于較大彎矩作用的影響，使墻體的破壞形態可能為大偏心或小偏心受壓破壞。

    (2)邊框柱截面較小時(MLQT-Ml系列墻體)，除邊框柱配筋率為3％的墻體之外，其余墻體均發生小偏心受壓破壞。邊框柱截面較大時(MLQT—M3系列墻體)，當邊框柱配筋率較大時，則發生小偏心受壓破壞。邊框柱截面適中時(MLQT—M2系列墻體)，當邊框柱配筋率小于l％時，破壞為小偏心受壓破壞。

    可見，邊框柱截面尺寸及配筋率是墻體破壞形態的主要影響因素。為防止發生小偏壓破壞，應控制邊框柱截面最小尺寸及配筋率的上下限。同時，在滿足承載力及剛度要求的基礎上，邊框柱截面尺寸不宜過大。

3、結論

    (1)密肋復合墻體的剪跨比、邊框柱截面尺寸及配筋率是承載力、破壞形態、截面應力應變特征的主要影響因素。較大剪跨比復合墻體的破壞模式為以兩側邊框柱破壞為主要破壞特征的彎曲破壞。

    (2)墻體的彎曲破壞形態可分為大偏心受壓破壞和小偏心受壓破壞兩種。這兩種破壞形態破壞特征的本質區別在于彎曲破壞時受拉側邊框柱翼緣鋼筋是否屈服。小偏心受壓破壞由于破壞時受拉側邊框柱翼緣鋼筋未屈服，不僅不經濟，而且具有脆性破壞的特征，設計上應予以避免。為此，工程設計中應采取措施限制墻體邊框柱截面最小尺寸及配筋率的上下限。

    (3)墻體在壓彎極限狀態時的截面正應變分布已不符合平截面假定。但兩側邊框柱邊緣應變基本符合平截面假定。

參考文獻

[1]西安建筑科技大學建筑工程新技術研究所．密肋壁板輕型框架結構理論與應用研究[R]．西安：西安建筑科技大學，2000  

[2]賈英杰．中高層密肋壁板結構計算理論及設計方法研究[D]．西安：西安建筑科技大學，2004

[3]黃煒．密肋復合墻體抗震性能及設計理論研究[D]．西安：西安建筑科技大學，2004

[5]王愛民．中高層密肋壁板結構密肋復合墻體受力性能及設    計方法研究[D]．西安：西安建筑科技大學，2006

[6]江見鯨．鋼筋混凝土非線性有限元分析[M]．西安：陜西科  學技術出版社，1994

(本文來源：陜西省土木建筑學會  文徑網絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)