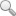橋梁墩柱基于性能的抗震設計方法

朱晞  江輝

北京交通大學 北京100044

引言

    最近十多年來，淺源地震(如1995年日本阪神地震、l999年我國臺灣地區(qū)的集集地震、2008年我國四川的汶川地震等)導致靠近活動斷層區(qū)域極為慘重的震災后果，引起了各國抗震界的高度關注。出于地震災害的教訓和對傳統(tǒng)抗震設計方法的深刻反思，在 Bertero等學者初步研究的基礎上，美國加州結構工程師聯(lián)合會(Stmetural Engineers Association of Califomia，SEAOC)提出了基于性能的地震工程(Peffomaance—Based Seismic Engineerin9，簡稱PBSE)和基于性能的抗震設計(Performance—Based Seismic Design，簡稱PBSD)的概念和理論框架。此后，美國應用技術委員會(Applied Technology Council，ATC)發(fā)布的ATC-34[和ATC-40報告、美國聯(lián)邦緊急事務管理局(Federal Emergency Management Agency， FEMA)發(fā)布的FEMA273和FEMA274報告中，都包含了大量基于性能抗震設計的思想。在我國，于2004年頒行的《建筑工程抗震性態(tài)設計通則》(CECSl60：2004)中，也初步體現(xiàn)了建筑結構基于性能的抗震設計思想。

    對于靠近活動斷層區(qū)的近場地震動而言，對建筑和橋梁結構同時存在高能量和大變形的需求，有必要同時考慮二者對結構抗震性能的影響。翟長海、謝禮立(2006)以集集地震近場記錄為基礎的研究表明，在中短周期頻段由近場速度脈沖型地震動給出的強度折減因子顯著小于一般地震動給出的強度折減因子，說明將現(xiàn)有的強度折減因子(都是遠場地震動給出的)應用到近場地區(qū)可能是不合適的。以預期性能指標為控制參數(shù)的強度折減因子模型，探討發(fā)展一種能夠同時考慮近場脈沖型地震動能量耗散和大變形需求的橋梁墩柱基于性能的抗震設計方法。

1、橋梁結構抗震設計性指標的確定

    對橋梁結構進行基于性能的抗震設計，首先應該明確劃分其抗震性能水準和性能指標。在性能指標的界定方面，Park等(Y.J.Park和R.S.An9，1985)從9座實際地震下遭受不同程度破壞的結構中，分析得到了損傷指數(shù)DI(由Park—An9雙參數(shù)模型確定)與破壞等級的關系，將DI=0.4作為可修復破壞的臨界值，當DI>1．0(后改為DI>0．8)時，視作結構倒塌。Hindi和Sexsmith(2001)根據(jù)鋼筋混凝土橋墩在地震動循環(huán)加載下的損傷性能分布特征，給出如表1所示的損傷指數(shù)與破壞等級間關系，用于定義結構在不同預期損傷狀態(tài)下的具體度量值。

表1 Hindi和Sexsmith建議的破壞等級

    為了考慮地震設防水準和結構性能指標間的關系，潘龍在參照對比鋼筋混凝土建筑結構不同震害等級的損傷指數(shù)范圍以及地震設防水準的基礎上，給出了如表2所示的鋼筋混凝土橋梁結構不同地震水平的損傷性能指標。合理性能目標的確定，有賴于震害觀測資料和實驗數(shù)據(jù)的積累，且和地震設防水準和預期性能要求密切相關，還需要大量的研究工作。

表2鋼筋混凝土橋梁結構不同地震水平的損傷性能指標

2、與抗震規(guī)范相容的基于性能指標的非彈性位移設計譜

    為了確定橋梁結構的自振周期，需要給出與抗震設計規(guī)范相容的基于性能指標的非彈性位移設計譜。為了和各規(guī)范動力放大系數(shù)譜相融合，本文采用間接方法計算非彈性位移譜，即通過對彈性位移譜進行合理的折減，而得出可用于設計的非彈性設計譜。

    對于彈性SDOF系統(tǒng)，相對譜位移與絕對譜加速度之間存在如下關系：

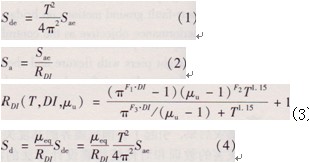
    式中：Sae和Sde分別為相應于周期T和某一固定黏滯阻尼比的彈性譜加速度與譜位移。而對非彈性SDOF系統(tǒng)，確定性能指標的非彈性譜加速度與彈性譜加速度之間存在下列近似關系：式中：RDI所提出的基于確定性能指標的強度折減因子RDI。式中：DI為結構的預期性能指標；μu為結構單調(diào)加載延性變形能力，F1、F2、F3為回歸參數(shù)。則由式(1)和式(2)可得確定性能指標的非彈性位移：

    式中：μeq為與性能指標相對應的等效延性系數(shù)(由式5定義)，即可由式(4)推導出以預期性能指標為控制參數(shù)的非彈性位移設計譜。圖1給出了根據(jù)美國UBC97規(guī)范Zone4區(qū)SA、Sc、SD三類場地、斷層距為2～5 km的動力放大系數(shù)譜計算的確定性能指標的非彈性位移譜。由于本文所建議RDI的有效周期范圍為0.2～4s，與此相對應，這里所得的非彈性位移譜最大有效周期也為4 s，更長周期范圍有待進一步研究。

圖1基于UBC97規(guī)范的確定性能指標的非彈性位移譜(5％阻尼比)

3、橋梁墩柱基于性能的抗震設計方法

    結構抗震設計方法經(jīng)歷了由原來的單一設防水準一階段設計逐漸發(fā)展到雙水準或三水準設防兩階段設計、三階段設計，以至多水準設防、多性能目標準則的基于結構性能的設計的發(fā)展過程。從本質(zhì)上來說，基于性能的結構抗震設計方法是對人們早有共識的多級抗震設防思想的進一步細化，通過將抗震設防目標和設計過程直接相聯(lián)系，從而更準確地把握結構在不同地震動水平下的實際性能。發(fā)展基于結構性能的實用抗震設計方法，需要解決一系列問題，如何將性能目標落實為具體的可以度量的性能指標并貫穿到抗震設計的過程中是最核心的問題之一。

    基于性能指標的強度折減因子，在所推導的非彈性位移譜的基礎上，提出如下橋梁結構基于性能思想的抗震設計方法流程，將性能目標貫穿到設計過程當中，而不是簡單的事后驗算。

    (1)提出結構的預期性能指標DI并計算等效變形延性根據(jù)橋梁的重要性程度、場地的地震動設防水準和業(yè)主的需求確定橋墩的預期性能指標DI；根據(jù)結構構造要求與荷載情況確定墩頂質(zhì)量m、墩高H；選取材料參數(shù)：混凝土軸心抗壓強度f′e，鋼筋屈服強度 fy鋼筋混凝土彈性模量E；根據(jù)材料和結構類型確定結構的極限延性變形能力μu；結合基于Park—Ang模型的改進損傷評估模型，按不同的預期性能狀態(tài)推導出結構等效變形延性系數(shù)μeq：

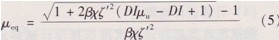
    式中：β為能量效應權重因子，按照Park—Ang模型的建議通常取為0.15；χ為結構滯回耗能與地震輸入能量之比；ζ′為結構累積輸入能量與最大變形間的等效變形速度比。圖2給出了根據(jù)式(5)計算的在給定損傷性能指標下考慮近場地震動累積能量效應的結構等效變形延性需求。圖3給出了由式(5)計算的等效延性系數(shù)和Fajfar所建議的等效延性因子模型[15]的對比，表明在同樣的結構單調(diào)變形能力下，近場地震動所容許的變形限值更小。

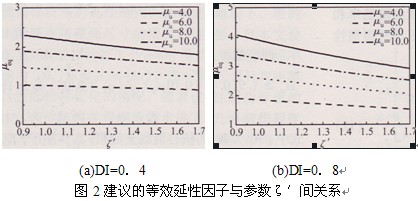
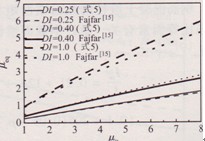
圖3建議的等效延性因子和Fajfar模型對比

    (2)計算目標位移△d

    △d與結構的形式以及設計極限狀態(tài)(預期性能目標)有關，在橋梁墩柱的抗震設計中，容許位移可根據(jù)結構的幾何要求(如支承長度)確定，以確保相鄰橋跨不會發(fā)生碰撞或相反運動而導致落梁，可參照Calvi等給出的如下公式估計：△d=δH(6)式中：δεsy為漂移比，可按下式確定：δ=μeqΦYH/3(7)其中Φy =λεsy /D(8)式中：εsy為鋼筋的屈服應變，可取為2％。；D為根據(jù)經(jīng)驗和構造初始假定的截面高度；λ為無量綱系數(shù)，依賴于橋墩截面首次屈服時受壓區(qū)的厚度以及非線性彎矩一曲率圖上屈服曲率的位置，Calvi等建議取為1.5。

    (3)確定結構自振周期

    根據(jù)場地類型、預期設計性能指標叫和目標位移限值△d，由確定性能指標的非線性位移設計譜(圖1)查出結構基階自振周期Te，對于阻尼比ξ不同的結構，可參照各規(guī)范方法進行阻尼折減。Te = f/(，△d，ξ)(9)

    (4)計算設計地震力

    根據(jù)場地類型和設防水準選擇設計地震動水平(本文中選取UBC97規(guī)范設計譜作為彈性加速度設計譜)，根據(jù)設計性能指標對彈性設計譜進行非彈性強度折減，由下式確定期望設計水平力Fd和墩底設計彎矩Md：Fd=m·αg·β(T,ξ)/RDI(T，DI,μu) (10)Md =Fd·H(11)式中：αg 為所在場地設計地震峰值加速度，β(T,ξ)為由設計規(guī)范給出的對應周期的動力放大系數(shù)。

    (5)進行截面設計、配筋

    鋼筋混凝土墩柱的截面慣性矩與縱向配筋率和軸壓比等因素有關，設計中截面慣性矩用開裂慣性矩Ier：

    式中：Ier為受拉鋼筋屈服時開裂截面的抗彎慣性矩；Ig為毛截面的抗彎慣性矩；Pl為縱向含筋率；P為軸力；Ac為墩柱截面面積。對于以彎剪變形為主的墩柱，截面開裂慣性矩Ier可由下式導出：

    其中：Keff為橋墩等效剛度。根據(jù)所得到的設計彎矩Md和合理的軸壓比ηk，調(diào)整橋墩截面初始幾何尺寸。

    縱向鋼筋：由所估計的截面幾何尺寸和對應的軸壓比，可由式(12)導出縱向配筋率的計算公式：

    Kowalsky等建議的經(jīng)濟配筋率范圍為0.7％≤Pl≤4％，我國《鐵路工程抗震設計規(guī)范》(GB50111一2006)也規(guī)定：墩身主筋全截面配筋率不應小于0.5％，也不宜大于4％。如果縱向配筋率不在此范圍內(nèi)，則應調(diào)整所設定的截面幾何尺寸從第(2)步重新計算。

    箍筋：橫向箍筋在延性橋墩中起到三方面的作用：①約束塑性鉸區(qū)混凝土；②提供抗剪能力；③防止縱向鋼筋壓屈。配箍率與截面延性要求有關，先由結構等效延性系數(shù)μeq確定截面曲率延性系數(shù)μφ ，可按下式計算：

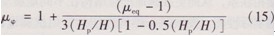
    式中：Hp為墩中塑性鉸長度，與塑性變形的發(fā)展和極限壓應變有很大關系，試驗結果離散性大，目前主要由經(jīng)驗確定，可按下式計算[20]：Hp = 0.08H＋0.022fyds (16)其中：fy為縱向鋼筋的屈服強度(N/nm²)；ds為縱向鋼筋的直徑(m)。對于箍筋，歐洲規(guī)范(Eurocode8)根據(jù)截面的延性系數(shù)μφ給出了如下的配筋公式：

    矩形截面：

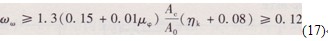
    圓形截面：

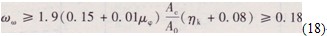
    式中：AO為截面的核心混凝土面積；ωω為力學配箍率，體積配箍率可按下式計算：Pω =ωωf′/fy(19)以上配筋公式考慮了箍筋對混凝土的約束效應，以確保墩柱塑性鉸區(qū)的變形和耗能能力。

    (6)校核與驗算

    進行延性設計能力方面的驗算，包括截面抗剪、防止縱向鋼筋屈曲與非塑性鉸區(qū)抗彎能力等的驗算。

    從上述基于性能指標的橋梁墩柱迭代抗震設計過程可以看出，本文所建議方法結合了反應譜法和基于位移抗震設計方法的優(yōu)點，同時又能夠有效地將性能指標貫穿到設計過程當中。

4、設計實例

    選用與UBC97規(guī)范對應的Sc類場地設計鋼筋混凝土橋梁墩柱，設計烈度為9度(0.4g)，橋墩墩頂質(zhì)量取為m=200t，墩高的容許范圍為6～15m，墩柱混凝土軸心抗壓強度為40 MPa，縱筋屈服強度為400 MPa，箍筋屈服強度為235 MPa，鋼筋混凝土彈性模量E為31.62 GPa，橋墩阻尼比為5％，混凝土保護層厚度取為截面直徑的l/20。設定橋墩的預期性能指標為DI=0.2、0.4、0.6和0.8來進行截面抗震設計，以分別代表橋墩“微小損傷”、“中等破壞”、“嚴重破壞”和“接近倒塌”四種不同的性能狀態(tài)。

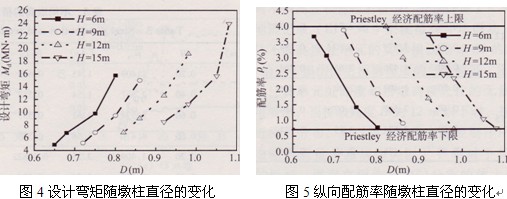
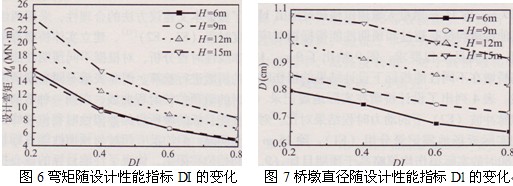
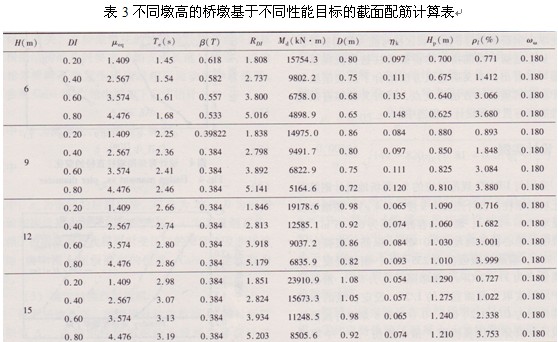
    表3給出了在固定軸力的前提下，對應于不同的墩高，根據(jù)不同的性能指標選取不同的橋墩直徑進行配筋計算的設計結果。圖4至圖7是基于UBC97規(guī)范設計譜由本文建議方法設計得到的圓形等截面橋墩的抗震設計結果。由表3配箍率的計算可看出。所有墩高和截面尺寸計算出的配箍率都為力學配箍率的下限值0.180，說明在小軸壓比的情況下，墩柱變形以彎曲為主，配箍率只要滿足構造要求即可。圖4給出了不同性能指標條件下設計彎矩隨墩柱直徑增大的變化情況，隨橋墩截面直徑的變大，設計彎矩也相應增大，且墩高越大，橋墩設計彎矩也越大。圖5反映了縱向配筋率隨墩柱直徑的變化，在固定軸力的前提下，橋墩高度越高，為使橋墩達到相同的性能指標所需的直徑越大，在確定的墩高下，墩的縱向配筋率隨截面尺寸的增大迅速降低，且本文設計的實際配筋率均處于Priestley等建議的經(jīng)濟配筋率范圍內(nèi)(0.7％≤Pl≤4％)。圖6給出了設計彎矩隨設計性能指標變化的情況，隨著設計性能指標值的增大，表示結構在預期地震水準下的允許損傷程度上升，不同墩高墩柱的設計彎矩分布規(guī)律相同，均以較大幅度下降。圖7討論了各種高度橋墩的設計直徑隨性能指標的關系，隨DI的提高，結構的抗震性能要求降低，橋墩直徑隨之下降，體現(xiàn)了基于性能抗震設計思想的合理性。

5、算例橋墩的實際地震動及模擬脈沖波時程檢驗

    為了驗證本文建議方法的合理性，采用兩組地震動加速度時程(E1、E2)，建立實體橋墩有限元模型進行非線性時程分析，對根據(jù)不同預期性能指標設計所得的橋墩進行驗算。圖8表示不同高度橋墩在各種直徑時的墩頂位移時程曲線，在同一種墩高時，不同設計性能目標的墩所得的彈塑性時程位移峰值之間差別較為明顯，但均沒有超過與預期性能目標相對應的結構初始位移限值，體現(xiàn)了性能目標的核心控制作用。當DI=0.60時，從圖中可以看出，四種高度橋墩的直徑分別為0.68m、0.75m、0.86m、0.98m時，其最大彈塑性位移依次為0.114m、0.173m、0.226m和0.337m，除l5m墩最大墩頂位移超過限值11.4％外，其他橋墩均沒有超過和預期性能指標相對應的位移限值，可滿足工程要求。圖9給出了9m、12m、15m高橋墩在不同性能指標下設計結果的損傷時程均值曲線。表4列出了設計橋墩在實際地震記錄(E1)和模擬脈沖波(E2)下的動力時程結果對比。對本文選用的實際近場地震記錄分組(E1)，除l5m墩在 DI=0.80時的實際損傷均值略高于預期目標(9．4％)外，其他所有高度橋墩的時程分析結果均沒有超過預期性能指標，但隨著橋墩高度的增大而趨于接近預期性能目標；而對于四條模擬脈沖記錄分組(E2)，對12m和15m高度橋墩在高損傷性能指標下的損傷均值則略大，但也都在15％的范圍內(nèi)，原因在于本文模擬脈沖的周期Tp和橋墩自振周期Te相接近而存在放大效應。總體來看，模擬脈沖的計算結果和實際記錄較為接近，模擬脈沖和實際記錄的時程分析結果證明本文建議方法能基本控制橋墩的實際損傷在預期性能指標的范圍之內(nèi)。

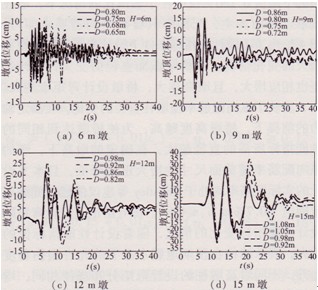
圖8各種墩高不同直徑時墩頂位移時程曲線(由E2模擬脈沖計算)

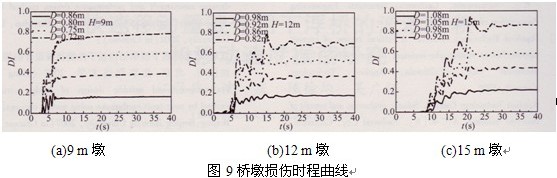
表4設計橋墩的實際地震記錄和模擬脈沖波的動力時程檢驗結果

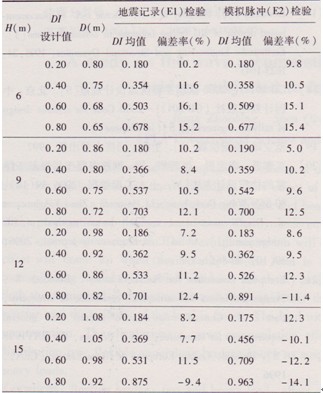
注：表中“一”號表示時程分析結果均值高于預期性能目標值。

圖10橋墩損傷均值沿橋墩高度分布

    對不同高度和直徑的橋墩，分別計算了4條實際近場地震記錄(E1)和4條模擬脈沖地震動(E2)下墩體不同高度處單元的實際損傷指標DI的均值：圖10給出了損傷值沿橋墩高度的分布特征，圖中5，為表示計算單元處高度和橋墩高度之比的無量綱參數(shù)。可看出，當橋墩高度H為12m以下時，損傷大體接近梯形分布，和以第一階模態(tài)起控制作用的低矮橋墩輸人能量分布規(guī)律類似；而對于高度為15m的橋墩，則存在損傷不均勻分布的放大效應．應是多階模態(tài)共同作用的結果，表明對于長細比更大的高柔橋墩和非規(guī)則全橋結構，有必要考慮多階模態(tài)效應的影響。

6、結論

    針對有高能量輸入和大變形需求的近斷層地震動，結合當前獲得廣泛關注的基于性能的抗震設計思想，本文融合反應譜法和基于位移設計方法的優(yōu)點，推導了和UBC97抗震設計規(guī)范相容的確定性能指標的非彈性位移譜，發(fā)展了一種橋墩結構直接基于性能指標的抗震設計方法，將結構的預期性能指標貫穿到抗震設計的全過程當中。以不同高度和預期性能目標的RC橋墩為對象，進行了截面設計和配筋計算，并用近場記錄和等效模擬脈沖進行了橋墩非線性時程驗算，驗證了本文方法適用于以彎、剪變形為主的中、低高度橋墩，對于高橋墩和非對稱全橋結構，則還需要進一步研究。

(本文來源：陜西省土木建筑學會  文徑網(wǎng)絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)