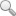陜西土木建筑網(wǎng)首頁 > 學(xué)術(shù)研究 > 課題研究 > 單層平面索網(wǎng)幕墻結(jié)構(gòu)玻璃與索網(wǎng)協(xié)同工作的動(dòng)力性能研究

摘要：采用模型試驗(yàn)和理論分析的方法對單層平面索網(wǎng)玻璃幕墻結(jié)構(gòu)玻璃與索協(xié)同工作的動(dòng)力性能進(jìn)行研究。首先通過結(jié)構(gòu)自振特性試驗(yàn)研究玻璃對于索網(wǎng)結(jié)構(gòu)頻率、振型以及阻尼的影響，然后提出了動(dòng)力荷載作用下玻璃與索網(wǎng)的協(xié)同工作機(jī)理，據(jù)此建立玻璃與索網(wǎng)協(xié)同工作的數(shù)值模型，采用該模型從理論上分析了結(jié)構(gòu)的自振特性。理論分析和試驗(yàn)結(jié)果表明：玻璃的抗彎效應(yīng)對結(jié)構(gòu)第一階模態(tài)影響較小，對結(jié)構(gòu)的高階模態(tài)影響比較明顯；索網(wǎng)+玻璃結(jié)構(gòu)的阻尼遠(yuǎn)大于索網(wǎng)的阻尼，玻璃幕墻結(jié)構(gòu)的阻尼比主要是由玻璃提供的。...

單層平面索網(wǎng)幕墻結(jié)構(gòu)玻璃與索網(wǎng)協(xié)同工作的動(dòng)力性能研究

馮若強(qiáng) 花定 興武岳 沈世釗

(1．哈爾濱工業(yè)大學(xué)深圳研究生院  廣東深圳518055；2.深圳市三鑫特種玻璃技術(shù)股份有限公司   

廣東深圳518054；  3.哈爾濱工業(yè)大學(xué)空間結(jié)構(gòu)研究中心  黑龍江哈爾濱l50090)       

引言

    單層平面索網(wǎng)支承式玻璃幕墻結(jié)構(gòu)，是近年來在國內(nèi)外應(yīng)用較為廣泛的一種新型幕墻結(jié)構(gòu)，具有建筑造型美觀、構(gòu)件輕巧纖細(xì)、視覺通透性好等優(yōu)點(diǎn)，因而特別適用于大型公共建筑中。與傳統(tǒng)的單層曲面索網(wǎng)結(jié)構(gòu)相比，單層平面索網(wǎng)幕墻結(jié)構(gòu)大多不具有負(fù)高斯曲面形式，因而結(jié)構(gòu)在平面外方向的剛度偏柔，表現(xiàn)出較明顯的幾何非線性特征。此特點(diǎn)決定了單層平面索網(wǎng)幕墻結(jié)構(gòu)的力學(xué)性能不同于傳統(tǒng)的線性結(jié)構(gòu)。   

    一般認(rèn)為預(yù)應(yīng)力玻璃幕墻結(jié)構(gòu)的力學(xué)性能是由索支承結(jié)構(gòu)決定的，玻璃不參與結(jié)構(gòu)工作。然而對于平面索網(wǎng)結(jié)構(gòu)，由于整個(gè)體系的剛度更多地依賴于索的幾何非線性，結(jié)構(gòu)變形較大，因而是否需要考慮玻璃對結(jié)構(gòu)整體的剛度貢獻(xiàn)就值得探討了。國內(nèi)外目前對于這個(gè)問題的研究不多，對于玻璃參與工作后對結(jié)構(gòu)力學(xué)性能尤其是動(dòng)力性能的影響缺乏了解。文獻(xiàn)僅討論了玻璃參與工作對于單層平面索網(wǎng)幕墻結(jié)構(gòu)靜力性能的影響，而單層平面索網(wǎng)玻璃幕墻結(jié)構(gòu)在實(shí)際工作環(huán)境中主要是受垂直于幕墻面的橫向動(dòng)力作用，如風(fēng)荷載和地震荷載。為此，本文首先通過結(jié)構(gòu)自振特性試驗(yàn)研究了玻璃對于索網(wǎng)結(jié)構(gòu)頻率、振型以及阻尼的影響，對玻璃與索網(wǎng)協(xié)同工作下的動(dòng)力性能進(jìn)行了研究，同時(shí)提出了動(dòng)力荷載作用下玻璃與索網(wǎng)的協(xié)同工作機(jī)理，據(jù)此建立了玻璃與索網(wǎng)協(xié)同工作的數(shù)值模型，采用該模型從理論上分析了結(jié)構(gòu)的自振特性，理論計(jì)算結(jié)果和試驗(yàn)結(jié)果吻合較好。

一、玻璃與索網(wǎng)協(xié)同工作機(jī)理

    單層索網(wǎng)玻璃幕墻結(jié)構(gòu)在構(gòu)造上包括預(yù)應(yīng)力拉索、連接爪件、玻璃面板3部分。玻璃的4個(gè)角點(diǎn)通過爪件和索連接，玻璃和玻璃之間采用硅酮密封膠連接。其傳力路徑為：風(fēng)荷載"玻璃面板"連接爪件"預(yù)應(yīng)力拉索"基礎(chǔ)或主體結(jié)構(gòu)。玻璃參與工作方式與連接爪件的形式密切相關(guān)，本文的試驗(yàn)和理論分析主要是針對夾片爪件進(jìn)行的，夾片爪和玻璃的具體連接形式如圖l所示，玻璃是通過壓板夾于爪件中的，在爪件和玻璃之間是不能傳遞拉力的。

 

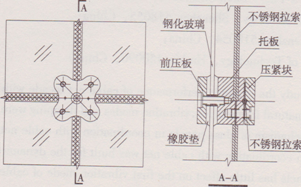
圖1玻璃和夾片爪連接示意圖

    動(dòng)力荷載作用下，對于采用夾片爪的單層索網(wǎng)玻璃幕墻結(jié)構(gòu)，玻璃與索網(wǎng)的協(xié)同工作表現(xiàn)在兩個(gè)方面，即玻璃對于索網(wǎng)結(jié)構(gòu)剛度的影響和對阻尼的影響。玻璃對于索網(wǎng)結(jié)構(gòu)的阻尼影響是指，填充玻璃間縫隙的硅酮密封膠的緩沖作用以及玻璃爪件與玻璃間的橡膠墊片的機(jī)械摩擦作用會(huì)在一定程度上消耗結(jié)構(gòu)振動(dòng)的能量，這相當(dāng)于為索結(jié)構(gòu)提供了附加阻尼。

    玻璃對于結(jié)構(gòu)剛度的影響：荷載作用下結(jié)構(gòu)變形較大。和玻璃4個(gè)角點(diǎn)連接的索節(jié)點(diǎn)在風(fēng)荷載作用下變形后的位置很可能不在同一平面內(nèi)，但實(shí)際上玻璃通過自身抗彎剛度的調(diào)節(jié)作用減少了各角點(diǎn)間的位移差別，使結(jié)構(gòu)的位移發(fā)展得更均勻；同時(shí)玻璃還會(huì)改變風(fēng)荷載在4個(gè)角點(diǎn)上的分配情況，使得風(fēng)荷載按照彈性支承的剛度分配到各個(gè)索節(jié)點(diǎn)上，上述作用可概括為是，相當(dāng)于起到靜不定屋面板的作用。

    根據(jù)上述玻璃參與結(jié)構(gòu)工作方式，采用有限元計(jì)算軟件ANSYS，對單層索網(wǎng)幕墻結(jié)構(gòu)玻璃與索網(wǎng)的協(xié)同工作進(jìn)行數(shù)值模擬。索采用linkl0單元，鋼結(jié)構(gòu)邊框采用beam4單元，玻璃采用shell63單元，爪件米用beaml88單元。數(shù)值模擬的關(guān)鍵是玻璃和夾片爪之間的連接，需要滿足一定的條件：①玻璃和爪件間為鉸接，在玻璃平面外方向上二者位移協(xié)調(diào)；②在玻璃平面內(nèi)方向上二者之間不能傳遞拉力。為此本文采取措施包括：①爪件和玻璃之間的連接處在玻璃平面外方向上采用自由度耦合來實(shí)現(xiàn)該方向上二者位移協(xié)調(diào)條件；②在玻璃平面內(nèi)方向上采用combin39彈簧單元來模擬玻璃和夾片爪之間的連接，彈簧的剛度為小量，彈簧的拉力接近于零。

二、試驗(yàn)?zāi)Ｐ秃驮囼?yàn)方案

    本文分別進(jìn)行了索網(wǎng)模型和索網(wǎng)加玻璃模型的自振特性試驗(yàn)，通過比較兩個(gè)模型的自振特性來研究玻璃對于結(jié)構(gòu)動(dòng)力性能的影響。通過實(shí)測兩種模型的阻尼比探討了玻璃對于結(jié)構(gòu)阻尼的影響。   

    2．1試驗(yàn)?zāi)Ｐ驮O(shè)計(jì)

    選取的試驗(yàn)?zāi)Ｐ蛻?yīng)具有較大工程實(shí)際意義，該模型下一步還要進(jìn)行振動(dòng)臺(tái)試驗(yàn)。考慮振動(dòng)臺(tái)性能參數(shù)、節(jié)點(diǎn)零部件和鋼化玻璃的加工條件，確定結(jié)構(gòu)模型的外軸線尺寸為2．81 m×2．81 m，玻璃的分格為0·365 m×0．365 m，鋼化玻璃厚度為4 mm，索采用 Ф03直徑不銹鋼絞線，彈性模量為1．03×los MPa。幾何相似比λL取l：4，可確定試驗(yàn)原型的參數(shù)如表1所示，試驗(yàn)?zāi)Ｐ统叽缛鐖D2所示。考慮振動(dòng)臺(tái)的試驗(yàn)條件，試驗(yàn)?zāi)Ｐ秃驮�型的加速度相似比取�?/span>1，則可確定試驗(yàn)?zāi)Ｐ秃驮�型�?dòng)力相似常數(shù)之間的關(guān)系如表2

表1結(jié)構(gòu)原型參數(shù)

    注：軸線，玻璃分格，厚度和索直徑單位m，彈性模量單位MPa。

    模型邊框?yàn)?/span>2．91 m×2．91 m的正方形框架，采用150 mm×8 mm的方鋼管。模型底部和振動(dòng)臺(tái)鉸接，同時(shí)為保證模型的在水平方向上的剛度，分別在模型頂部的邊梁上采用銷拴連接了三道支撐，如圖3所示，支撐采用l00 mm×5 mm方鋼管，支撐的布置位置、支撐和邊框的截面需要滿足使邊框剛度對索網(wǎng)振動(dòng)頻率的影響在0．5％以下。

 

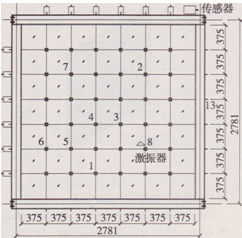
圖2試驗(yàn)?zāi)Ｐ统叽缂暗谝浑A模態(tài)測點(diǎn)布置

表2相似常數(shù)之間關(guān)系

 

 

圖3框架側(cè)視圖和俯視圖

    2．2試驗(yàn)及加載方案

    試驗(yàn)?zāi)Ｐ头譃閮煞N，索網(wǎng)模型和索網(wǎng)+玻璃模型，如圖4、圖5所示。通過比較索網(wǎng)模型和索網(wǎng)+玻璃模型的自振特性來考察玻璃對于結(jié)構(gòu)動(dòng)力性能的影響。玻璃對結(jié)構(gòu)自振特性的影響可以通過比較兩個(gè)模型的頻率和振型來加以體現(xiàn)，玻璃對結(jié)構(gòu)阻尼的影響可以直接通過測量兩個(gè)模型的阻尼比獲得。框架位移通過位移計(jì)采集，其量程為±150 mm。位移、加速度和索拉力的數(shù)據(jù)通過兩臺(tái)國產(chǎn)16通道動(dòng)態(tài)波譜儀采集。結(jié)構(gòu)的阻尼比采用了自由振動(dòng)和正弦激振兩種方法測得，正弦激振器應(yīng)避免布置于被測振型的反彎點(diǎn)處，而應(yīng)布于結(jié)構(gòu)中部振型較大的位置，綜合考慮選取點(diǎn)8作為激振點(diǎn)，如圖2所示。結(jié)構(gòu)自振振型測點(diǎn)布置的原則是，要放置于該振型的波峰、波谷以及體現(xiàn)振型特點(diǎn)的部位，因此要隨著測量振型的不同而改變位置。

 

圖4索網(wǎng)模型

 

圖5索網(wǎng)+玻璃模型

三、自振特性結(jié)果分析

    考慮到單層平面索網(wǎng)結(jié)構(gòu)具有一定的幾何非線性，其頻率和結(jié)構(gòu)的振動(dòng)幅值相關(guān)，本文首先研究小振幅情況下索網(wǎng)模型和索網(wǎng)+玻璃模型的自振特性，此時(shí)結(jié)構(gòu)為線性，下一節(jié)研究大振幅情況下結(jié)構(gòu)的自振特性。小振幅下結(jié)構(gòu)的振動(dòng)幅值為結(jié)構(gòu)跨度的1／250。

    本文還根據(jù)上文中提出的動(dòng)力荷載作用下玻璃與索網(wǎng)的協(xié)同工作機(jī)理建立了有限元數(shù)值模型來計(jì)算兩個(gè)試驗(yàn)?zāi)Ｐ偷淖哉裉匦裕�有限元模型如圖6、圖7所示。

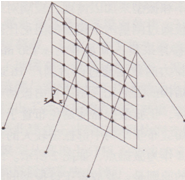
圖6索網(wǎng)有限元模型

 

圖7索網(wǎng)+玻璃有限元模型

    3．1線性自振特性結(jié)果

    兩個(gè)模型第一階模態(tài)的測點(diǎn)布置圖，如圖2所示，分別將自由振動(dòng)法和共振法測得的兩個(gè)模型的第一階模態(tài)的阻尼比、頻率和振型，同采用有限元計(jì)算得到的結(jié)構(gòu)頻率和振型進(jìn)行了比較，如表3所示。有限元計(jì)算得到兩個(gè)模型的第一階振型如圖8、圖9所示。兩個(gè)模型的自由衰減曲線如圖10、圖ll所示。從上述表中和圖中可見：兩種實(shí)測方法得到的結(jié)構(gòu)阻尼比基本一致，說明采用共振法得到的結(jié)構(gòu)阻尼比是可以滿足精度要求的，同時(shí)索網(wǎng)+玻璃模型的阻尼比遠(yuǎn)大于索網(wǎng)模型的阻尼比；索網(wǎng)+玻璃模型的頻率比索網(wǎng)模型的頻率大4．8％，玻璃剛度對于結(jié)構(gòu)的第一階模態(tài)的影響不大，兩個(gè)模型的振型差別較小；三種方法得到結(jié)構(gòu)的基頻和振型比較一致。

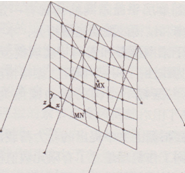
圖8索網(wǎng)模型第一階振型

 

圖9索網(wǎng)+玻璃模型第一階振型

 

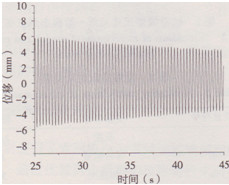
圖10索網(wǎng)模型自由振動(dòng)衰減曲線

 

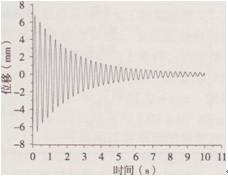
圖11索網(wǎng)+玻璃模型自由振動(dòng)衰減曲線

表3各種方法結(jié)構(gòu)第一階模態(tài)自振特性比較

    由于兩個(gè)模型的第二階模態(tài)和第三階模態(tài)、第五階模態(tài)和第六階模態(tài)、第七階模態(tài)和第八階模態(tài)、第九階模態(tài)和第十階模態(tài)的頻率較為接近，試驗(yàn)只能激起第一、三、四、六、八、十階模態(tài)。兩個(gè)模型的各階振型測點(diǎn)布置圖相同，限于篇幅本文只列出了第三、四、六振型的測點(diǎn)布置圖，如圖l2～14所示。

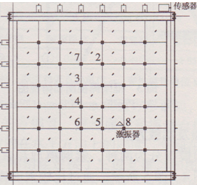
圖12第三階模態(tài)測點(diǎn)布置圖

 

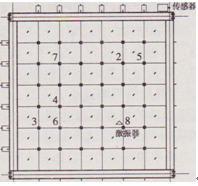
圖13第四階模態(tài)測點(diǎn)布置圖

 

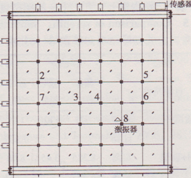
圖14第六階模態(tài)測點(diǎn)布置圖

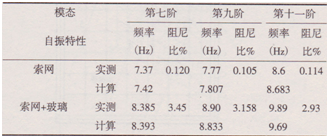
    表4列出了第三、四、六振型下共振方法測得索網(wǎng)+玻璃模型和索網(wǎng)模型的阻尼比、頻率和振型，并同有限元計(jì)算結(jié)果進(jìn)行了比較。而對于七、九、十一階模態(tài)則只列出了結(jié)構(gòu)的頻率和阻尼比，如表5所示。從表中可見：索網(wǎng)模型的阻尼比都在0．1％附近，和文獻(xiàn)[10]較為接近，索網(wǎng)+玻璃模型的阻尼比遠(yuǎn)大于索網(wǎng)模型的阻尼比，其阻尼比主要由玻璃提供；各階模態(tài)下索網(wǎng)+玻璃模型的頻率比索網(wǎng)模型的頻率大9．6％～l5％，玻璃附加剛度對于高階模態(tài)的影響比第一階模態(tài)明顯，主要原因是結(jié)構(gòu)的高階模態(tài)的振型曲線變化明顯，變形的曲率較大，此時(shí)玻璃的局部剛度作用會(huì)比較明顯；此外兩個(gè)模型的振型在數(shù)值上有一定差別；兩種方法得到結(jié)構(gòu)的基頻和振型比較一致，說明本文的實(shí)測結(jié)果是正確的，有限元模型能夠較好地反映結(jié)構(gòu)實(shí)際的力學(xué)性能。上述兩種模型的自振特性比較說明，玻璃+索網(wǎng)模型的阻尼主要由玻璃提供的阻尼決定，玻璃的附加剛度對于結(jié)構(gòu)高階模態(tài)的頻率有一定影響。

表4索網(wǎng)模型和索網(wǎng)+玻璃模型的第三、四、六階模態(tài)自振特性比較

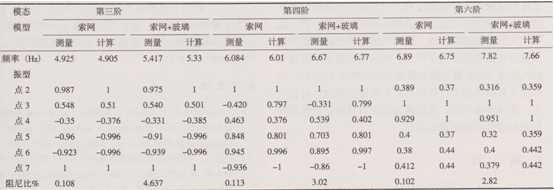
表5結(jié)構(gòu)第七、九、十一階模態(tài)自振特性比較

 

    3．2非線性自振特性結(jié)果分析

    上節(jié)研究了小振幅情況下的索網(wǎng)模型和索網(wǎng)+玻璃模型的自振特性，本節(jié)則對大振幅情況下兩個(gè)模型的自振特性進(jìn)行了比較，此時(shí)結(jié)構(gòu)具有一定的幾何非線性，頻率和結(jié)構(gòu)的振動(dòng)幅值相關(guān)。受到激振器功率的限制，共振法僅能保證索網(wǎng)+玻璃模型第一、三、四和六階振型共振時(shí)結(jié)構(gòu)振幅達(dá)到結(jié)構(gòu)跨度的1／65，其余更高階振型則遠(yuǎn)小于該值，而對于索網(wǎng)結(jié)構(gòu)則可保證前四階振型振幅達(dá)到l／50跨度。在振幅為1／65跨度時(shí)兩個(gè)模型試驗(yàn)測量和有限元計(jì)算結(jié)構(gòu)前四階模態(tài)頻率和振型的比較如表6所示。有限元計(jì)算求解結(jié)構(gòu)非線性振動(dòng)頻率的方法為非線性有限元時(shí)程方法，即給結(jié)構(gòu)以一定幅值的初始位移(該初始位移的分布模式和結(jié)構(gòu)的振型相同)讓結(jié)構(gòu)作無阻尼自由振動(dòng)，通過結(jié)構(gòu)的位移響應(yīng)時(shí)程曲線直接計(jì)算出結(jié)構(gòu)的非線性振動(dòng)頻率。

表6索網(wǎng)模型和索網(wǎng)+玻璃模型的結(jié)構(gòu)第一、三、四和六階模態(tài)自振特性比較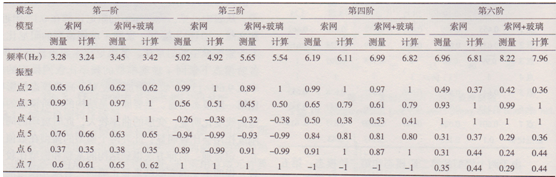

    從表中可見：兩個(gè)模型第一階模態(tài)的振型基本相同，索網(wǎng)+玻璃模型的頻率比索網(wǎng)模型的頻率大5．2％，和線性自振分析基本相同，玻璃剛度對于結(jié)構(gòu)的第一階模態(tài)的貢獻(xiàn)不大；其他各階模態(tài)下索網(wǎng)+玻璃模型的頻率比索網(wǎng)模型的頻率大l2．5％～l8．1％．玻璃附加剛度對于其他各階模態(tài)的影響比線性自振時(shí)要略微明顯，這說明結(jié)構(gòu)位移增大后，玻璃參與結(jié)構(gòu)工作程度增加，玻璃剛度對于結(jié)構(gòu)動(dòng)力性能影響略有增加；兩種方法得到結(jié)構(gòu)的頻率和振型比較一致，說明本文的實(shí)測結(jié)果正確，同時(shí)有限元模型能夠較好地反映結(jié)構(gòu)的非線性力學(xué)性能。當(dāng)結(jié)構(gòu)位移從小振幅為結(jié)構(gòu)跨度l／250增加到大振幅為結(jié)構(gòu)跨度1165時(shí)，玻璃剛度對結(jié)構(gòu)動(dòng)力性能影響只有略微的增加。可以認(rèn)為，非線性振動(dòng)時(shí)，玻璃附加剛度對結(jié)構(gòu)動(dòng)力性能的影響和線性振動(dòng)時(shí)基本相同。

四、結(jié)論

    本文首先通過結(jié)構(gòu)自振特性試驗(yàn)對玻璃與索網(wǎng)協(xié)同工作的動(dòng)力性能進(jìn)行了研究，然后提出了動(dòng)力荷載作用下玻璃與索網(wǎng)的協(xié)同工作機(jī)理，并據(jù)此進(jìn)行了相應(yīng)的理論分析，試驗(yàn)結(jié)果和理論分析結(jié)果表明：

    (1)動(dòng)力荷載作用下，單塊玻璃的抗彎效應(yīng)對結(jié)構(gòu)第一階模態(tài)影響較小，對結(jié)構(gòu)的高階模態(tài)影響比較明顯，主要原因是結(jié)構(gòu)高階模態(tài)的振型曲線變化明顯，局部曲率較大，此時(shí)玻璃對局部剛度影響比較明顯。

    (2)索網(wǎng)+玻璃結(jié)構(gòu)的阻尼比可達(dá)3．5％左右，遠(yuǎn)大于索網(wǎng)的阻尼比，這說明玻璃幕墻結(jié)構(gòu)的阻尼比主要是由玻璃提供的，顯然這對于抑制結(jié)構(gòu)產(chǎn)生較大的動(dòng)力響應(yīng)是有利的。

參考文獻(xiàn)

[1] Vyzantiadou M A,Avdelas A V. Point fixed glazing systems:  technological and morphological aspects  [J]. Journal of     Constructional Steel Research, 2004,60(6): 1227-1240

[2]馮若強(qiáng)．單層平面索網(wǎng)玻璃幕墻結(jié)構(gòu)靜動(dòng)力性能研究[D]．哈爾濱：哈爾濱工業(yè)大學(xué)，2006 [3]石永久，吳麗麗，王元清，等．點(diǎn)支承玻璃建筑單層索網(wǎng)柔性支承體系及其工程應(yīng)用[J]．工業(yè)建筑，2005，35(2)1—5

[4] Schlaich J, Schober H, Moschner T. Prestressed cable net facades  [Jj.Structural Engineering International, 2005,15  ( 1 ):36-39

[5] Feng Ruoqiang, Wu Yue, Shen Shizhao. Simplified calculation    method of nonlinear frequency of cable net under mean wind    load [J].Acta Mechanica Solida Sinica, 2006, 19(3):248- 254

[6]馮若強(qiáng)，武岳，沈世釗．單層平面索網(wǎng)幕墻結(jié)構(gòu)的風(fēng)激動(dòng)力 性能研究[J1．哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2006，38(2)：153—1 56

[7] Feng Ruoqiang, Wu Yue, Shen Shizhao. Working mechanism  of single-layer cable net supported glass curtain walls [J].International Journal of Advances in Structural Engineering,2007,10(2):183-195

[8]馮若強(qiáng)，武岳，沈世釗．單索幕墻體系中的玻璃與索協(xié)同工作機(jī)理研究[J]．西安建筑科技大學(xué)學(xué)報(bào)，2006，38(5)：  619—623

[9]馮若強(qiáng)，武岳，沈世釗．考慮玻璃參與工作的單層平面索網(wǎng) 幕墻結(jié)構(gòu)靜力性能研究[J]．建筑結(jié)構(gòu)學(xué)報(bào)，2005，26(4)： 99—106

[10]曹資，薛素鐸，劉景園，等．索網(wǎng)屋蓋結(jié)構(gòu)阻尼特性試驗(yàn)研究[J]．地震工程與工程振動(dòng)，1995，15(2)：92—99

(本文來源：陜西省土木建筑學(xué)會(huì)     文徑網(wǎng)絡(luò)：呂琳琳  尹維維 編輯   文徑 審核)

上一篇： 鋼管混凝土梁側(cè)向沖擊荷載動(dòng)力響應(yīng)的試驗(yàn)研究和數(shù)值模擬

下一篇： 從汶川地震看提高建筑結(jié)構(gòu)抗倒塌能力的必要性可行性