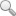陜西土木建筑網首頁 > 學術研究 > 課題研究 > 高應變動力試樁中重錘一樁一巖土沖擊響應的理論研究

摘要：為研究高應變動力試樁中重錘與樁土體系的匹配關系，基于一維行波理論，采用連續桿件模型，建立了研究高應變動力試樁中重錘一樁一巖土沖擊響應問題的數值計算模型與算法，用數值分析的結果定量評價了重錘激發樁周及樁端巖土阻力的能力，以及高應變動力試樁中錘重、落距、樁墊剛度、樁徑、樁長、巖土性質對檢測承載力的影響，從而明確了選擇試驗錘重時應考慮的各種因素，并用數值分析的結果驗證了重錘上測力的新方法的可行性。采用8×10，kg與14×10，kg試樁重錘分別以o．8 m與o．5 m的落距沖擊試驗樁進行現場試驗，試驗以及數值分析的結果從實踐和理論兩個方面有效支持了“重錘低擊”原則。...

高應變動力試樁中重錘一樁一巖土沖擊響應的理論研究

陳久照  溫振統   李   廷   張希朝

(廣東省建筑科學研究院，廣東廣州510500)

一、引言

    傳統的高應變法波動方程分析程序是以樁上部實測的樁身物理量為邊界條件，用行波理論采用數值法反演分析求解波動方程，從而獲得動力試樁過程中巖土對樁的阻力及樁身阻抗變化狀況。

  前人有在實驗室條件下，用數值模擬的方法研究不同的地質條件及其他主要相關參數對打樁過程及樁的承載力的影響，但并沒有用數值模擬的方法模擬高應變動力試樁中重錘與樁及巖土的動力響應過程。美國PDl公司開發的GRLWEAP軟件用于分析柴油錘的打樁性能，樁的計算模型為離散質彈模型，本文采用的樁模型為連續桿件模型。

    本文的基本思路是：假定錘重、落距已知，樁周、樁底土的力學模型及參數、樁的物理參數、幾何尺寸為已知條件，運用行波理論，采用數值計算的辦法，求解錘一樁體系在沖擊過程中，錘體的受力，以及各樁單元的位移和各土單元被激發的最大靜阻力，進而模擬樁上部單元實測的物理量(用傳感器實測)，并定量地評價重錘激發樁周及樁底巖土阻力的能力及影響因素，將錘體受力與樁身第一單元受力作比較可驗證重錘上測力的新方法的可行性。

    高應變動力試樁中“重錘低擊”原則是指：為了保證樁受沖擊過程中獲得足夠大的能量，且不致在樁頂產生過高的錘擊應力，應適當采用較重的錘與較低的落距m。本文用數值計算和現場試驗結果來驗證此原則。

二、重錘一樁一巖土沖擊響應分析計算模型與算法

    2．1基本假定

    (1)重錘視為剛體；

    (2)樁為一維線彈性桿件(不考慮樁身阻抗變化)；

    (3)樁墊為無質量的彈簧：

    (Kd為樁墊剛度，Ed、Ad、Ld分別為樁墊的彈性模量、面積及厚度)；

    (4)土為黏彈塑性體(土模型在2．2．3中詳述)；  

    由于錘的重力與沖擊過程中樁對錘的作用力相比很小，忽略不計；

    在計算步長Δt時間內，錘的受力隨時間呈線性變化(線性加速度假設)；

    速度和位移——向下為正，向上為負；  

    應力——壓應力為正，拉應力為負；   

    錘體受力——向下為正，向上為負。

    2．2沖擊響應計算模型與算法

    將樁離散為長度為l m的若干桿件單元，土阻力作用于各單元的底部，土的力學行為用黏彈塑性體來模擬。

    數值計算的時間步長：

    其中：c為樁身材料彈性波速。

    圖中：U(r，j)為重錘在jΔt時刻的位移；F(r，j)為重錘在jΔt時刻的受力；V(r，j)為重錘在jΔt時刻的速度；R(r，．j)為i單元j時刻的土阻力。

    2．2．1錘體沖擊過程中受力算法

    (1)j=1即t=Δt時刻錘、樁各物理量算法：

    由于錘體與樁頂接觸前，錘體呈自由落體運動，

    式中：h為重錘落距；V(r，O)為重錘在jΔt=0時刻的速度。

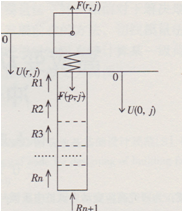
 圖1重錘與樁沖擊響應示意圖

    忽略樁墊的變形時間，從重錘與樁墊接觸時開始計時．此時錘的位移：

 

    式中：U(0，j)為jΔt時刻樁頂面位移；V(0，j)為jΔt時刻樁頂面速度；F(0，j)為jΔt時刻錘對樁頂面的作用力；Fd(o,j)為jΔt時刻樁頂面的下行波；磊為樁的力學阻抗。

    (2)中間值算法： 

    t=jΔt時刻

    ①F(r，j)=-F(0,j)

    ②樁墊的壓縮量等于錘體位移與樁頂面位移之差

    (樁頂面不可能對錘產生向下的作用力)    (11) 

    t=jΔt時刻，各變量如下：

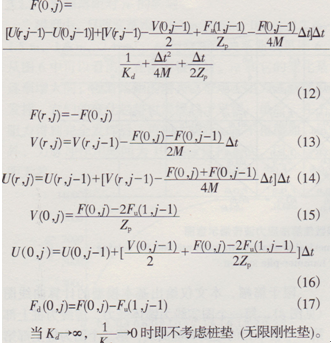
    上式中：Fd(i，j)為i單元j時刻的下行波；Fu(i，j)為i單元．j時刻的上行波；F(i，j)為i單元j時刻的受力；V(i，j)為i單元j時刻的運動速度；U(i，j)為i單元j時刻的位移。

    2．2．2計算截止時刻

    當時F(r,j)>≥0時，計算截止，即樁頂不可能對錘產生向下的力。

    2．2．3沖擊過程中土阻力的計算模型

    土為黏彈塑性體，因此土對樁的運動阻力可分為兩個部分：動阻力Rd(i,j)與靜阻力Rc(i,j)。

    各單元土的極限靜阻力及彈性極限Qu(i)均為已知量，樁單元i在j時刻的靜、動阻力分別為：

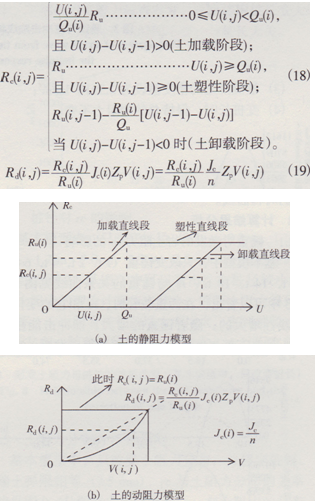
 圖2土的靜阻力和動阻力模型

    2．2．4應力波在樁中的傳播規律

    只考慮土阻力作用引起的應力波變化，不考慮樁身阻抗變化，不考慮樁身材料阻尼

    式中：n為樁單元數，i=n+1對應樁端土阻力；kΔt為  沖擊開始后計算的截止時間。

    圖3示意圖取3個樁單元(樁長3 m)為例，表示重錘一樁一土動態響應的數值解法中，應力波傳播的過程。

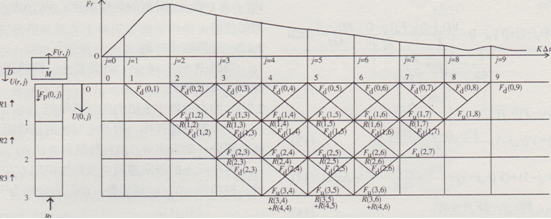
 圖3重錘與樁沖擊響應特征線數值解法應力波傳播示意圖

三、數值計算內容及計算結果分析

    3．1數值計算內容

    高應變動力試樁中重錘激發的土阻力rc受很多因素的影響，包括錘重、落距、樁墊剛度、樁徑、樁長、樁側土及樁端土的彈限、土的極限阻力、阻尼系數等參數。為了探討各參數對rc的影響規律，我們進行了大量的計算分析。為了進行有效的對比，先假定一個錘一樁一土基本模型，在進行計算時，一般每次都只改變一個參數，而保持其他參數不變，這個基本模型如圖4所示，并作如下假設：

    (1)樁側土單位面積的側土阻力從樁頂到樁底呈線性(增大)變化，樁底土單位面積的端阻力不變；

    (2)樁側土每一單元的彈限、阻尼系數都相等；

    (3)樁混凝土的密度值設為2．5x103 kg／m³；

    (4)變樁長時，保持總的側阻力不變。

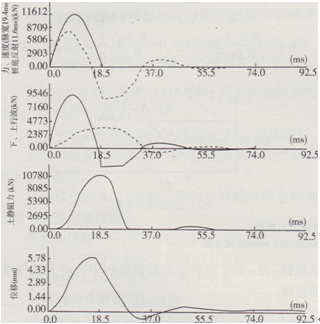
圖4重錘沖擊響應理論計算結果

    基本模型中各參數的選擇，是為保證樁周土阻力完全發揮而采用盡量小的錘重、落距等參數。再增大錘重、落距等參數l'C不會再增大，而減小錘重、落距等參數時rc會相應減小。

    基本模型參數值取為：

    落距l．5 m，錘重14x103 kg，樁徑1．4 m，樁長20．0 m，波速3460 m／s，Kd為400 MPa·m，rc為10780 kN，土的彈限Qu為2．5 mm、土的極限靜阻力 Ru樁側為28—560 kN、樁端為4900 kN；土的Case阻尼系數上的取值分別為：樁側l．0，樁端o．2，rc理論值10780 kN。

    限于篇幅，本文僅給出基本模型的計算曲線圖(見圖4)，第一個圖實線為錘體受力，虛線為樁上部第一個樁單元的速度響應曲線，第二個圖為樁上部第一個樁單元的上下行波時程曲線，第三個圖為土的靜阻力的時程曲線，第四個圖為樁上部第一個樁單元位移的時程曲線。

    3．2計算結果分析

    3．2．1錘重對激發的巖土阻力rc的影響

    基本模型中，只改變錘重(1 t，2t，4t，6t，8t，11 t，14 t，18 t)，rc與錘重的關系曲線見圖5。從圖5中可以看出，在錘重較輕時，rc和它的變化幾乎是線性增大的；隨著錘重的增大，即沖擊能量的增加，樁身下部與樁端土的阻力逐漸得以發揮，它們的變化趨勢也慢慢趨于平緩；最后，在土阻力得到完全發揮后，再加大錘重，rc不再增加。從計算曲線上可以看到，當錘重較輕時，樁底反射明顯，錘重增加后樁底反射越來越弱，因此，在保證足夠沖擊能量的前提下，用窄脈沖進行樁身完整性的評價更合適。另外，隨著錘重增加，力脈沖作用時間顯著增加。

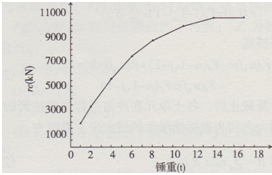
圖5激發土阻力與錘重的關系曲線(基本模型中。只改變錘重)

    3．2．2重錘落距對TC的影響

    模型中，只改變落距(03 m，0．6m，0．9m，1．2 m，  1．5 m，1．8 m，2．1 m)，rc與落距的關系曲線見圖6。從圖6中可以看出，在落距較低時，rc和它的變化是  逐漸增大的；隨著落距的增大，樁周土阻力逐漸得以發揮，它們的變化趨勢也慢慢趨于平緩；最后，在土阻力得到完全發揮后，再加大落距，rc不再增加。另外，力脈沖作用時間為19.4ms保持不變，因tr與落距無關。

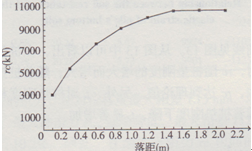
圖6激發土阻力與落距的關系由線(基本模型中，只改變落距)

    3．2．3樁徑對rc的影響

    基本模型中，只改變樁徑(0．5 m，0．8 m，1．1 m，1．4 m，1．7 m．2．0 m，2．3 m，2．6 in)，rc與樁徑的關系曲線見圖7。從圖7中可以看出，在樁徑較小時，極限土阻力的理論計算值也較小，因而土阻力得到充分發揮，rc也隨著樁徑的增大而增大，直到樁徑達到1．6 m左右；隨著樁徑的進一步增大，rc反而有所減小，并慢慢趨于平緩。這說明，隨著樁徑的進一步增大，在基本模型中其他參數不變的情況下，樁端土阻力的發揮越來越受到限制。樁的剛度增大使重錘與樁的匹配能力下降，力脈沖寬度tr隨著樁徑增大而逐漸減小。

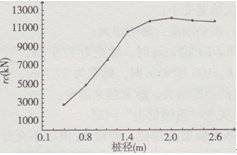
 圖7激發土阻力與樁徑的關系曲線(基本模型中，只改變樁徑)

    3．2．4樁長對FC的影響

    本模型中，只改變樁長(4 m，7 m，10 m，15 m，20 m，25 m，35 m，45 m)，rc與樁長的關系曲線見圖8。從圖8中可以看出，由于改變樁長并沒有改變總的樁側阻力及樁端力，rc并沒有隨樁長的改變而發生較大的改變。在樁長較短時(小于l5 m)，激發土阻力隨樁長而增加，樁長大于15 m后rc基本不變，原因可能是樁長較短時，樁的運動更近似剛體，沖擊能量更多地消耗在動阻力中。在計算模型中沒有考慮樁身材料本身對應力波能量的吸收，而實際上應力波在沿樁身傳播過程中存在能量衰減(路損)，應力波傳播路徑越長，這種變化越大，因此樁長變大時，樁中、下部的巖土阻力越難激發，rc也將因樁長變大而減小。另外力脈沖作用時間不變，與樁長無關。

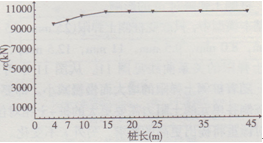
圖8激發土阻力與樁長的關系曲線(基本模型中，只改變樁長)

    3．2．5土阻力分布對rc的影響

    基本模型中，只改變土阻力分布，并假定樁側、樁端土彈限相等(2．5 mm)，rc與土阻力分布的關系曲線見圖9。從圖9中可以看出，rc與土阻力的分布無關。但是，一般情況下樁側土彈限小于樁端土彈限，在這種情況下，rc將隨端阻力的減小而增大(見圖l0)，即摩阻力比端承力更易激發，因此，對端承型樁(嵌巖樁除外，因為它的樁端彈限很小)，錘重的要求更高，另外tr不變化。

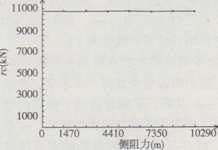
圖9激發土阻力與土阻力分布的關系曲線

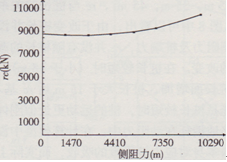
圖10激發土阻力與土阻力分布的關系曲線

    3．2．6樁側土彈限對rc的影響。

    基本模型中，只改變樁側土彈限(25 mm，35 mm，6．5 mm，8．0 mm，9．5 mm，11 mm，12．5 mm)，rc與樁側土彈限的關系曲線見圖ll。從圖11中可以看出，rc隨著樁側土彈限的增大而慢慢減小。即要充分激發樁側各單元的土阻力需要更大的樁一土相對位移，此時對錘重將提出更高的要求，另外tr不變化。

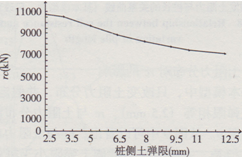
圖11激發土阻力與樁側土彈限的關系曲線    (基本模型中，只改變樁側土彈限)

   3．2．7樁端土彈限對／'c的影響

    基本模型中，只改變樁端土彈限(0．1 mm，0．5 mm，2．5 mm，3．5 mm，5．0 mm，10．0 mm，20．0 mm，40．0 mm)， rc與樁端土彈限的關系曲線見圖12。

    從圖l2中可以看出，在樁端土彈限小于2．5 mm時，樁周土阻力得以完全發揮，rc不變；在樁端土彈限大于2．5 mm以后，rc隨著樁端土彈限的增大而減小，在樁端土彈限大于樁頂最大位移后，rc就變得越來越平緩。對Q—S曲線呈緩變形的大直徑樁，由于樁端彈限大，對錘重的要求相當高，所以在行標中，對高應變動測在這類樁上的應用作了一定的限制，另外tr不變化。

    3．2．8樁墊剛度對rc的影響

圖12激發土阻力與樁端土彈限的關系曲線    (基本模型中，只改變樁端土彈限)

    基本模型中，只改變樁墊剛度，rc與樁墊剛度的關系曲線見圖l3。從圖l3中可以看出，在樁墊剛度較小時，rc隨樁墊剛度的增大而增大；隨著樁墊剛度的增大，rc達到理論值。另外，tr對樁墊剛度相當敏感，隨著樁墊剛度下降，tr顯著增加、

圖13激發土阻力與樁墊剛度的關系曲線(基本模型中，其他參數不變。只改變樁墊剛度)

    3．2．9力脈沖寬度t，的影響因素

    (1)錘重：影響大，錘重增加一倍，脈寬tr增寬約40％；

    (2)樁徑：有一定影響，隨著樁徑r的增大，樁剛度變大脈寬變小；

    (3)樁墊剛度：影響很大；

    當Kd=10 MPa·m時，脈寬為17．9 ms；  

    當Kd=100 MPa·m時，脈寬為27．7 ms；隨著Kd的不斷增大，脈寬越來越窄。

    3．2．10關于“重錘低擊”問題

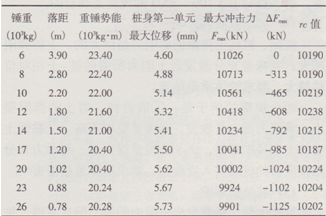
    以基本模型為基礎，降低Kd值以不充分激發土阻力，Kd取300 MPa·m，只改變錘重和落距，基本保證激發的rc不變(實際誤差小于l％)，計算結果見表1。

    從表l可看出，隨著錘重的增加、落距降低，在重錘的重力勢能略有下降的情況下，樁身第一單元最大位移逐漸增加，樁-土相對位移增大，更易激發巖土對樁的抗力，相對位移量最大相差l．13 mm，增加了24．5％；最大沖擊力Fmax逐漸降低，最大相差ll25 kN，減小了10．2％。因此，在激發土阻力rc相同的前提下，“輕錘高擊”易造成樁頂破壞的主要原因有三個：

    (1)“輕錘高擊”將在樁身上產生較大的峰值壓應力；

    (2)輕錘一般橫截面面積小，與樁頂面作用面積小，壓強大；

    (3)高落距會加劇錘的偏心沖擊，從而使樁頂受力不均勻而造成樁頂局部受壓破壞。

    表1錘重、落距與樁頂最大沖擊力的關系

四、工程實例

    廣東省佛山市南海區某鉆孔灌注樁工程，分別用8x103 kg與14x103 kg兩重錘分別以0．5 m與0．8 m落距對該工程208樁進行高應變沖擊試驗，部分實測信號如圖14、l5所示，各樁單元最大位移與錘重及落距關系如圖16所示

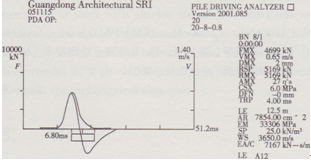
圖14 20#樁8×103kg錘0．8m落距高應變實測波形

圖15 20#樁14x103 kg錘0．5 m落距高應變實測波形

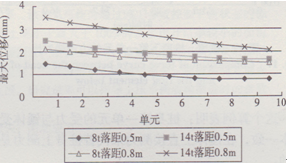
圖16各樁單元最大位移

    對于同一根樁，8x10，kg重錘以0．8 m落距所激發的單樁豎向承載力檢測值為5169 kN，最大應力值為4699 kN，而l4x103 kg重錘以0．5 m落距所激發的單樁豎向承載力檢測值為5635 kN，最大應力值為4588 kN，驗證了“重錘低擊”的原則。

    由圖l6中可以看出在相同的落距下l4x103 kg錘所激發的各樁單元的最大位移均比8×103 kg錘所激發的要大，因而也就能夠激發更大的樁周摩阻力和樁端阻力，從而獲得更高的單樁承載力檢測值。

五、上測力新方法的驗證

    高應變動力試樁傳統的測力方法是在樁身上用應變式傳感器測力，在《建筑基樁檢測技術規范》 (JGJ l06—2003)中提出了在重錘上安裝加速度計測力的新方法，下面通過一個算例分析來驗證這種測力新方法的可行性。

    大直徑灌注樁樁徑為1．4 m，樁長為20．0 m，彈性波速取3460 m／s，K。為400 MPa·m，重錘錘重14．0×103 kg，落距為l．5 m，rc為10780 kN，土的彈限Qu為2．5 mm、土的極限靜阻力Ru樁側為28"560 kN、樁端為4900 kN；土的Case阻尼系數Jc的取值分別為：樁側l．0，樁端0．2，rc理論值10780 kN。

    將計算所得到錘的受力(實線)和樁身上第一個單元(應變式傳感器大多數安裝在此)計算得到的力(虛線)繪在同一坐標中，從圖l7中可以看到兩條曲線是基本重合的(相位的微小差異是樁身第一單元的慣性造成的)，從而從理論上驗證了重錘上測力新方法的可行性。

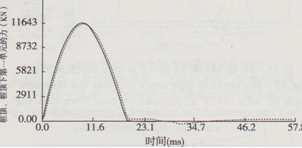
圖17樁頂、樁頂下第一單元的力曲線對比

    這個算例表明：樁身第一單元的受力與錘體受力基本一致，在錘體上直接測力來代替樁身上測力是可行的。

六、結論

    綜合前面分析計算的結果，高應變動力試樁中在試驗錘重選擇時應考慮下列因素：

    (1)檢測承載力及樁的承載性狀

    通過前面的分析，我們可以看到，除了應考慮總的承載力外，還應考慮樁的承載性狀，一般情況下，樁底彈限大于樁側彈限，這與土的破壞模式有關，樁側土壓剪破壞，樁底土壓密或刺入破壞。在承載力的構成中，若端阻力占的比例越大，則要求錘體重量越重，與JGJ l06--2003的規定相一致。

    (2)樁徑的影響

樁徑越大，樁本身的慣性越大，錘與樁的匹配能力下降，要求錘體重量越重，此外樁徑的增加也會增大土的彈限，這樣會導致對錘重要求的顯著增長。

    (3)樁長的影響

     在前面的算例中，沒有考慮應力波在樁中傳播時，樁材料本身對應力波的衰減作用，而實際上樁越長，應力波在傳播過程中的衰減(路損)也越多，樁中、下部及端阻力就越難充分激發，要求錘體重量越重。這一點與JGJ l06--2003的規定是吻合的。

    (4)巖土彈限的影響

    樁側、樁底土彈限的影響力是巨大的，土的彈限越大，意味著充分激發巖土阻力所需的樁一土相對位移越大，要求錘體重量越重。

    兩個極端的例子是：①嵌巖樁，巖土的彈限很小，承載力很容易激發，對錘重要求不高。②黏性土上的大直徑擴底樁，Q—S曲線呈緩變型，端承力充分激發所需的樁端貫人度很大，要求錘體重量很重[4]。  

    (5)樁墊的影響

    樁墊太軟，錘激發巖土阻力的能力明顯下降，樁墊太硬則達不到調整樁頂均勻受力，保護樁頭的目的。因此，樁墊的選擇應該是在保證充分激發巖土阻力的前提下，盡量選用較軟的樁墊。

    (6)提倡“重錘低擊”

    “輕錘高擊”雖然也可以提高沖擊能量，但在激發的承載力相近的條件下，輕錘高擊在樁身上產生較高的壓應力，且由于輕錘與樁作用面積小，加之高落距加劇錘擊的偏心，這些因素都會造成樁頂局部受力過大而破壞，因此在高應變動力試樁中應提倡“重錘低擊”。

    經過錘一樁一土的沖擊響應分析表明在沖擊過程中，樁身第一單元受力和錘體受力是基本一致的，因此在錘體上通過加速度計來測力的新方法是可行的。

參考文獻

[1]中華人民共和國行業標準．JGJ l06--2003建筑基樁檢測技術規范[s]．北京：中國建筑工業出版社，2003

[2]楊桂通，張善元．彈性動力學[M]．北京：中國鐵道出版社，l988

[3] CAPWAP for Windows Manual[M]．Pile Dynamics，Inc．2000

[4]陳凡，徐天平，陳久照，等．基樁質量檢測技術[M]．北  京：中國建筑工業出版社，2003

(本文來源：陜西省土木建筑學會     文徑網絡：呂琳琳  尹維維 編輯   文徑 審核)

上一篇： 從工程設計視角對船撞橋事故進行風險評估總體研究

下一篇： 鋼管混凝土梁側向沖擊荷載動力響應的試驗研究和數值模擬