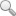陜西土木建筑網首頁 > 學術研究 > 課題研究 > 彎箱梁橋橫截面上預應力鋼束張拉次序研究

摘要：通過針對預應力張拉次序對箱梁變形及結構受力影響的理論分析，并結合計算結果，給出了針對彎箱梁預應力張拉施工的“先外后內，對稱均衡”的彎箱梁橫截面上的張拉次序原則。通過施工過程中的監(jiān)控及后期監(jiān)測，效果較好，研究成果對彎箱梁橋預應力鋼束張拉具有一定的參考價值。...

彎箱梁橋橫截面上預應力鋼束張拉次序研究

林偉偉  吳志勤  丁漢山  歐慶保  王立海

東南大學，江蘇南京210096 上二海國康聯同橋梁工程咨詢有限公司 上海200092

江蘇潤揚大橋發(fā)展責任有限公司 江蘇鎮(zhèn)江212002

引言

    目前曲線梁橋在現代化的公路及城市道路立交中的數量逐年增加，應用已非常普遍。尤其在互通式立交的匝道橋設計中應用更為廣泛。預應力混凝土彎箱梁橋，其預應力鋼束的線形大部分為空間三維曲線，具有雙向曲率，這使得彎箱梁橋在預應力作用下的內力分析較為困難。目前國內對彎箱梁橋仍多采用梁單元來進行分析，一般不考慮預應力鋼束在梁截面上的橫向位置。由于彎箱梁的曲線形式，預應力作用會產生與彎橋的曲率半徑大小直接相關的徑向水平分力、扭矩和扭轉變形，而由于內側腹板中鋼束的平面半徑比外側的平面半徑小，其空問長度和空間彎角及孔道摩阻損失不同。另外，后續(xù)預應力鋼束的張拉對前面已張拉的預應力鋼束也有較大影響。因此，相同的張拉控制力，內外側預應力鋼束在梁體上產生的預應力效果就不同。由于內外側預應力對彎箱梁梁體所產生的內力和變形存在很大差異，所以預應力施T過程中，對于彎箱梁不能簡單地套用直箱梁的兩側對稱張拉方式。若預應力鋼束張拉的先后順序掌握不好，可能會導致彎箱梁在施工階段出現過大的側向彎曲和扭轉變形，嚴重的可能引起箱梁側向開裂甚至破壞。因此對預應力混凝土連續(xù)彎箱梁橋的預應力鋼束張拉次序進行研究很有必要。本文以潤揚長江公路大橋世業(yè)洲互通匝道實際工程為研究背景，采用大型有限元分析軟件Ansys建立相應的有限元模型，結合實際施工情況，提出幾種典型的預應力張拉方案，在分析模型上進行模擬張拉，通過比較幾種不同的張拉次序下結構的響應，提出曲線箱梁橋預應力鋼束較合理的張拉次序，對于類似的彎箱梁橋的建設也有重要的參考價值。

1、有限元模型的建立

    1.1工程概況

    潤揚長江公路大橋世業(yè)洲互通D匝道橋，平面曲率半徑R=60m。該橋上部結構跨徑為4×32.604m，四跨一聯。橋寬8.66～8.75m，橋長130.417m。采用單箱單室截面。梁高210cm，頂、底板厚25cm，跨中及支座附近腹板厚度為40cm和60cm。下部結構采用200cm X382cm的矩形墩。從0號到4號橋墩，橋墩高度依次為34.952m，36.089m，37.211m，38.071m，38.243m。對于橋墩支座，l～3號橋墩內外側支座皆設置為固定支座；0號和4號橋墩外側支座設置為單向支座，內側支座設置為雙向支座。固定支座要求墩梁對應節(jié)點上各方向均不發(fā)生相對位移；單向支座要求墩梁對應節(jié)點的徑向及豎向變形一致；雙向支座只要求墩梁對應節(jié)點的豎向變形一致。該橋上部結構采用C50混凝土，下部結構墩身采用C30混凝土。預應力鋼筋采用符合ASTMA：416-92a的15.24mm高強低松弛鋼絞線。

    1.2單元選取及預應力作用的模擬

    潤揚長江公路大橋世業(yè)洲互通D匝道橋的有限

 

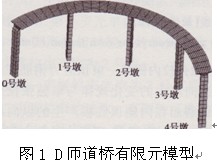
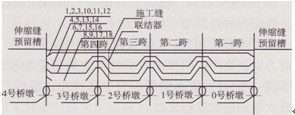
圖2 D匝道橋預應力鋼束構造簡圖

    元建模采用Ansys提供的實體單元SOLID95來模擬混凝土材料，采用三維桿單元LINK8進行模擬預應力鋼筋。

    在有限元中，常用的預應力加載有等效力法和等效應變法兩種形式。本文根據《公路鋼筋混凝土及預應力鋼筋混凝土橋涵設計規(guī)范》中對預應力損失作出的各項規(guī)定，計算得出各種因素造成的預應力損失。 將張拉應力扣除各種預應力損失便得到有效預應力。而后利用等效降溫法進行有效預應力的施加。T為施加的溫度；σ為有效預應力；E為預應力鋼束彈性模量；δ為預應力鋼束的線脹系數。

    1.3對支架的模擬

    該匝道橋的箱梁施工順序為：由4號墩向0號墩方向逐跨進行施工，箱梁采用滿堂支架施工。有限元模型中必須實現對梁體下部支撐即支架的模擬。支架在支撐梁體時，只可承受壓力而不可承受拉力，針對支架表現出的這種拉壓異性的特點，考慮采用非線性桿單元進行模擬。這種單元可以通過一些單元性質設定，將其設定為單向受力桿件。采用這種單元進行分析時，需要將其和上部梁體建立耦合聯結。當其受壓時，和普通線性桿件一樣，而當其軸力大于零時，它會出現斷裂，不再參與結構受力。本文采用LINKl0單元，將該單元的初應變值設為大于l，參數KEYOPT(3)=1，則該單元可以模擬只能承受壓力的支架。

2、張拉過程分析

    預應力鋼束布置如圖3所示，將所有預應力鋼束分為內側預應力鋼束和外側預應力鋼束兩部分，共18根，其中“張拉束”為第一施工階段(即圖2中4號墩至施工縫之間梁段)所需張拉的鋼束，即本文研究對象，“通過束”為本施工階段不需張拉的鋼束。施工過程中采用的是一次張拉一束預應力鋼束的張拉工藝，依次“張拉束”進行張拉。經計算分析，得到單獨張拉各預應力鋼束時箱梁頂板、底板縱向應力曲線圖，如圖4所示。

 

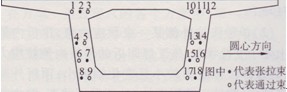
圖3預應力鋼束截面布置圖

 

(a)單獨張拉各鋼束時頂板內側縱向應力曲線圖

 

(b)單獨張拉各鋼束時頂板外側縱向應力曲線

 

(c)單獨張拉各鋼束時底板內側縱向應力曲線

 

(d)單獨張拉各鋼束時底板外側縱向應力曲線

圖4單獨張拉各鋼束時頂底板縱向應力曲線(單位：MPa)

可以得出以下結論：

    (1)單獨張拉內側某一束預應力束，頂板內側絕大多部位(除施工縫附近外)處于受壓狀態(tài)，跨中部位的壓應力大于梁兩端的壓應力；頂板外側則基本上處于受拉狀態(tài)，施工縫附近的頂板外側拉應力較大，其余部位拉應力較小且變化幅度小；底板內側基本上處于受壓狀態(tài)；底板外側局部受拉，最大拉應力為0．519MPa。

    (2)單獨張拉外側某一束預應力束，頂板內側基本上處于受拉狀態(tài)，施工縫附近的頂板內側拉應力較大，其余部位拉應力較小且變化幅度小；頂板外側絕大多部位(除施工縫附近外)處于受壓狀態(tài)，跨中部位壓應力大于梁兩端壓應力；底板內側局部受拉，最大拉應力為0.501MPa；底板外側基本處于受壓狀態(tài)。

    (3)單獨張拉內側某一束預應力鋼筋在外側頂底板產生的縱向應力的變化規(guī)律與單獨張拉外側某一根預應力鋼筋而在內側頂底板產生的縱向應力的變化規(guī)律基本一致。數值上，頂板內外側之間的應力差別大于底板內外側之間的應力差別。

    (4)單獨張拉同一側的不同預應力鋼束在頂底板產生的應力的差別很小(施工縫處除外)。

    由上述分析可知，若僅張拉一束預應力束，不同預應力束張拉產生的縱向應力總體上而言差別較小。為了進一步分析，取不同預應力束張拉在頂底板產生的最大縱向應力進行比較。

    由圖5(a)和圖5(b)可以看出，單獨張拉外側某一束預應力束在頂底板內側產生的縱向應力最大值均遠大于相應頂底板外側縱向應力最大值；與此對應，當單獨張拉內側某一束預應力束時，頂底板外側的縱向應力最大值均遠大于頂底板內側的縱向應力最大值。

 

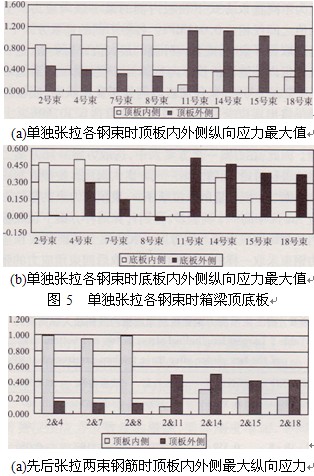
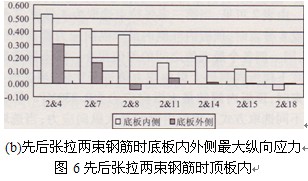
    單獨張拉某根預應力束時，頂板產生的縱向應力最大值均大于底板產生的縱向應力最大值。單獨張拉14號預應力束時，頂板外側縱向應力最大值為1.147MPa，為單獨張拉不同預應力束時頂底板內外側縱向應力最大值；單獨張拉2號預應力束時，頂底板內外側縱向應力最大值為0.861MPa，小于單獨張拉其他預應力束時所產生的頂底板內外側縱向應力最大值。

    由上述可知，第一步先單獨張拉2號預應力筋將在頂底板內外側產生相對較小的縱向應力值。因此建議第一束張拉束選取為2號束。

    當確定第一束張拉束選取為2號束后，接下來考慮的是第二束張拉束的選取。有兩種可選方案：

    (1)選取與2號束同一側的預應力束，即某一外側束；可供選擇的預應力束有4號束、7號束、8號束；

    (2)選取另一側的預應力束，即某一內側束。可供選擇的有11號束、14號束、15號束、l8號束。

    經計算，得到如下不同張拉預應力束時頂底板內外側最大縱向應力，如圖6(a)和圖6(b)所示。

    上述兩圖中，2號束對應的結果為先張拉2號束再張拉4號束的最大縱向應力，其余含義類似。

    由圖6(a)和圖6(b)可以看出，當第二束張拉束選取為與2號束同一側的預應力束時，其在頂板內側、底板內側以及底板外側所產生的最大縱向應力值均遠大于張拉束選取為內側束時所產生的相應應力值。當第二束張拉束選取為內側束時，不同的張拉束在頂板內外側產生的最大縱向應力比較接近，而在底板內外側產生的最大縱向應力變化相對較大。比較而言，第二束張拉束選為18號預應力束更為合理。

表1張拉方案

    綜合上面的分析可知，在張拉過程中可以遵循一定的規(guī)律，先張拉外側鋼束后張拉內側鋼束以及上下對稱張拉。在確定前兩束張拉束依次為2號束和l8號束的基礎上，依據上述張拉規(guī)律，在確定后續(xù)六束張拉束時可考慮如下六種可能的張拉方案：

    在方案一至方案六的各個方案中，第一束鋼束表示的是總的張拉順序中第三束將被張拉的鋼束。在第一束、第二束張拉束分別選取為2號束、18號束的基礎上，以上各方案皆把將進行張拉的第三束預應力束選取為與2號束同在一側的外側預應力束。為比較各種不同選取方式的差異，現將計算結果例于表2。

表2前三束預應力束張拉后頂底板內外側最大縱向應力

    由表2可見，當第三束張拉束選取為4號束、7號束或8號束時，頂板內外側的最大縱向應力都是拉應力，同一側各個最大值之問的差值很小。將不同選取方式下頂板內側最大縱向應力值進行比較，當選取8號束時，頂板內側的最大縱向應力為0.339MPa，該值為不同選取方式下頂板內側的最大縱向應力；當選取7號束時．頂板內側的最大縱向應力為0.296MPa，該值為不同選取方式下頂板內側的最小縱向應力。上兩值之間僅相差0.043MPa。各種不同的選取方式下，當選取8號束時，底板內外側的最大值皆為負值，這表明底板內外側沿橋長方向整體處于受壓狀態(tài)；當選取4號束或7號束時，僅底板內側處于受壓狀態(tài)，底板外側仍將出現拉應力，而且最大拉應力達0.307MPa。

    綜上所述，將第三束張拉束確定為8號束比較合理。因此，在方案一至方案六中，選取方案一和方案二繼續(xù)進行討論，而將方案三至方案六淘汰。按照方案一和方案二中所布置的張拉順序，一束預應力束的張拉對應Ansys中的一個荷載步，分別計算兩種方案下頂底板內外側縱向應力值。因方案一和方案二的前四束預應力鋼束采取一樣的張拉順序，故僅取后四束預應力的張拉結果進行比較。結果如表3所示，可以看出：

表3不同方案下頂底板縱向應力

 

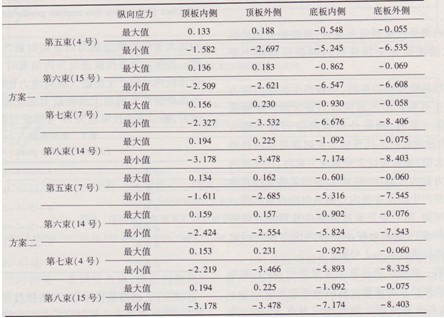
    (1)在后四束預應力束的張拉過程中，方案一和方案二中的頂板內外側的最大縱向應力皆為拉應力，而最小縱向應力皆為壓應力。此說明頂板內外側某些部位受拉而某些部位受壓。

    (2)在后四束預應力束的張拉過程中，方案一和方案二中的底板內外側的最大縱向應力皆為壓應力，而最小縱向應力亦皆為壓應力。這說明底板內外側整體處于受壓狀態(tài)。

    (3)第五束、第六束以及第七束張拉束選取不同的預應力束，張拉后的結果會有所不同，最大縱向應力絕對值很小，且彼此之間的差別亦非常小。最大的差值發(fā)生在方案一中第五束張拉束選取為4號束在頂板外側產生的最大縱向應力為0.188MPa，而方案二中第五束張拉束選取為7號束相應的最大縱向應力為0.162MPa，差值僅為0.026MPa；底板的最小縱向應力絕對值比較大，且彼此之間的差別相對較大。最大的差值發(fā)生在方案一中第五束張拉束選取為4號束在底板外側產生的最小縱向應力為一6.535MPa，而方案二中第五束張拉束選取為7號束相應的最小縱向應力為一7.545MPa，差值達到1.01MPa。

    (4)隨著總體張拉鋼束數量的增加，不同方案之間的應力結果差異減小，例如方案一和方案二中第五束、第六束的應力結果差異大于方案一和方案二中第七束的應力結果差異。當張拉完所有的預應力鋼束后，不同方案問的應力結果相同。

    綜合比較，方案二稍優(yōu)于方案一，因此建議對于潤揚大橋世業(yè)洲互通D匝道橋第一施工階段預應力的張拉采取先張拉2號束，而后依次張拉18號束、8號束、11號束、7號束、l4號束、4號束、15號束的張拉順序。

3、預應力張拉次序對彎箱梁變形的影響分析

    張拉布置在腹板上的預應力鋼束，會影響彎箱梁橋的曲率，且不同位置的鋼束對梁體的影響不同，張拉布置在內側腹板上的預應力鋼束會增加彎箱梁橋的曲率，而張拉位于外側腹板上的預應力鋼束則會減小彎箱梁橋的曲率。對于布置于同一截面上的預應力鋼束，通過計算結果分析可知，在橫截面上張拉這些預應力鋼束首先應盡量保證內、外側腹板上已張拉的預應力鋼束接近相等。在豎向上，建議根據曲率半徑選擇張拉束，即：曲率半徑大的彎箱梁，建議先張拉中間的鋼束，再張拉其上下的鋼束；當彎橋曲率較小時，建議先張拉外側頂板鋼束。通過上述有限元計算與理論分析，可以概括為“先外后內，對稱均衡”的張拉次序。

4、結束語

    本文以潤揚大橋世業(yè)洲互通D匝道橋為工程背景，研究了連續(xù)曲線箱梁橋預應力鋼束張拉次序問題。經計算分析，得出以下結論：

    (1)為了利用預應力抵消外荷載產生的扭矩，從理論上講可以采用下列措施：①內外側腹板上預應力鋼束線形對稱，但張拉力不同，外側張拉較內側的大；②在頂底板布置彎曲方向相反的預應力鋼束。

    (2)初始張拉束的選取對梁體應力影響較大，隨著張拉預應力束數量的增加，梁體剛度增加，不同張拉束的選取所產生的應力差異減小。

    (3)在曲線箱梁橋預應力鋼束張拉，應遵循“先外后內，對稱均衡”的張拉次序。

這些認識，在世業(yè)洲互通的設計施工過程中得到及時貫徹和應用，通過預應力張拉施工過程的監(jiān)控，以及成橋后三年來的多次觀測，證明效果良好，可供國內工程師在類似橋梁建設中參考。

參考文獻

[1]邵容光，夏淦．混凝土彎梁橋[M]．北京：人民交通出版，l994

[2]孫廣華．曲線橋計算[M]．北京：人民交通出版社，l995

[3]邢靜忠，王永崗，陳曉霞．ANSYS7．0分析實例與工程應用[M]．北京：機械工業(yè)出版社，2003

[4]  胡豐玲．連續(xù)彎箱梁橋預應力鋼束張拉次序研究[D]．南京：東南大學，2004

[5]  Samaan M，Kennedy J B，Sennah K．Dynamic analysis of curved continuous multiple—box girder bridges[J]．Journal of    Bridge Engineerin9，2007，12(2)：184—193

[6]  晏致濤，王繼成，李正良，等．后張法預應力混凝土空心板梁張拉有限元分析[J]．重慶建筑大學學報，2003，25(6)：62—66

[7]李新平，任華．曲線箱梁橋預應力作用的仿真分析[J]．華南理工大學學報：自然科學版，2004，32(12)：47—50

(本文來源：陜西省土木建筑學會  文徑網絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)

上一篇： 青藏鐵路凍土沼澤化斜坡濕地路基穩(wěn)定性研究

下一篇： 舊簡支梁轉變?yōu)檫B續(xù)梁的試驗研究