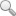陜西土木建筑網(wǎng)首頁(yè) > 學(xué)術(shù)研究 > 課題研究 > 斜索橋面耦合面內(nèi)參數(shù)振動(dòng)實(shí)例研究及參數(shù)分析

摘要：以南京長(zhǎng)江二橋A20拉索為研究對(duì)象，對(duì)《斜索橋面耦合面內(nèi)參數(shù)振動(dòng)理論模型》的理論方法進(jìn)行數(shù)值求解，驗(yàn)證近似理論解的正確性。足限幅特性。...

斜索橋面耦合面內(nèi)參數(shù)振動(dòng)實(shí)例研究及參數(shù)分析

任淑琰　 顧明

同濟(jì)大學(xué)土木工程防災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室　上海200092 上海林同炎李國(guó)豪土建工程咨詢有限公司　上海200092

引言

    本系列論文第一部分介紹了作者建立考慮拉索垂度、拉索重力的弦向分力及索張力沿索長(zhǎng)變化等因素的斜索一橋面等效質(zhì)量塊，在軸向簡(jiǎn)諧激勵(lì)下的響應(yīng)的理論模型及近似求解方法。本文以南京長(zhǎng)江二橋A20拉索為研究對(duì)象，對(duì)本系列論文的第一部分的理論方法進(jìn)行了數(shù)值求解，分析了激勵(lì)強(qiáng)度、拉索阻尼及拉索張力對(duì)響應(yīng)的影響。此外，本文除特別注明。

1、實(shí)例研究

    以南京長(zhǎng)江二橋中的最長(zhǎng)索A20為例進(jìn)行數(shù)值分析。南京長(zhǎng)江二橋A20拉索的基本參數(shù)為：拉索A、B兩錨固端之問(wèn)的弦長(zhǎng)L=330.4m，水平及垂直投影長(zhǎng)度l和 h分別為292.389m和153.859m；拉索單位長(zhǎng)度自重mg=0.795kN/m；拉索斷面面積A=0.01019m²；張力在B端(下端)的豎向分量K=3369.351kN，張力的水平分力Hs為6652kN；拉索彈性模量E=1.90×t08kN/m²。橋面節(jié)段等效質(zhì)量取值：092=0.334wl時(shí)，M=9000t；ω2=0.505ω1，M=3950t；,ω2=0．979ω1，M=1050t；ω2=1.980ω1，M=260t。此外，阻尼系數(shù)取為0.92 N·s/m，對(duì)應(yīng)的拉索一階阻尼比為0.19％。根據(jù)拉索運(yùn)動(dòng)方程(文獻(xiàn)[1]式(5))的系數(shù)計(jì)算得到斜拉索的一階頻率ω1=0．4654Hz。采用四階四段龍格一庫(kù)塔(Runge—Kutta)法[2]求解非線性耦合運(yùn)動(dòng)微分方程組(文獻(xiàn)[1]式(8))，得到索一橋耦合系統(tǒng)的響應(yīng)特性。拉索振幅隨頻率的變化反映了拉索參數(shù)共振最重要的特征。圖l為斜拉索一階模態(tài)和橋面的最大振幅隨兩者固有頻率比的變化。

 

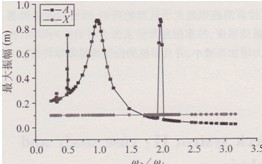
圖1斜拉索一階位移響應(yīng)和橋面位移

    由圖l可知：①在ω1/ω2．接近1/3、1/2、1和2時(shí)斜拉索一階振幅出現(xiàn)峰值，和文獻(xiàn)[1]的理論解一致，其中ω1/ω2≈1和ω1/ω2≈2時(shí)峰值較大，ω1/ω2≈l/2時(shí)峰值稍小，ω1/ω2≈l/3時(shí)峰值最小；②理論分析還指出，當(dāng)ω1/ω2≈3時(shí)可能會(huì)出現(xiàn)內(nèi)共振，而數(shù)值計(jì)算發(fā)現(xiàn)在ω1/ω2≈3斜拉索振幅雖然比初始擾動(dòng)值大，但并不明顯，這是由于引起ω1/ω2≈3的共振項(xiàng)為文獻(xiàn)[1]式(8)中的立方非線性項(xiàng)，且A20索的立方非線性項(xiàng)系數(shù)較小所致；③斜拉索一階振幅在1：3共振時(shí)對(duì)應(yīng)的峰值中心為ω1/ω2≈0.3344，滿足文獻(xiàn)[1]中的式(22)；在1：2和2：1共振時(shí)的峰值中心在ω1/ω2≈0.5047和1．9803處，滿足文獻(xiàn)[1]中的式(18)；④對(duì)于橋面而言，其振動(dòng)幅值和初始位移相同。此外，比較圖1與文獻(xiàn)[3]不考慮拉索重力弦向分力的有垂度索模型的計(jì)算結(jié)果可知，對(duì)于拉索的第一階模態(tài)，共振區(qū)分布以及共振區(qū)的峰值基本一致，這是因?yàn)?/span>A20索的垂度較小，斜拉索重力弦向分力的影響較小。

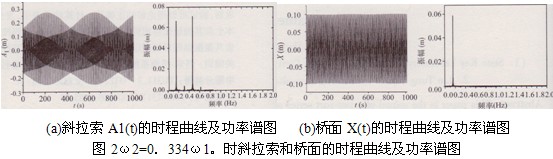
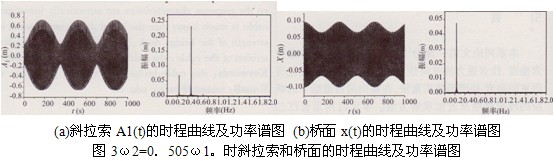
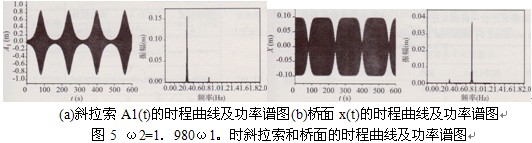
    圖2～圖5為不同頻率比(接近l：3、l：2、1：1以及2：1)時(shí)拉索一階位移A1(t)和橋面位移X(t)的時(shí)程曲線和相應(yīng)的功率譜圖。圖示結(jié)果表明：①在共振情況下斜拉索的振幅是有限值。因在各種共振情況下，系統(tǒng)振動(dòng)方程中的各系數(shù)滿足文獻(xiàn)[1]中的有界性條件(見(jiàn)文獻(xiàn)[1]中的式(28)、式(32)和式(37))。②斜拉索和橋面的幅值中均含有ωa、ωb。兩個(gè)頻率成分。在1：3、1：2以及2：1共振時(shí)斜拉索和橋面的幅值譜中均是靠近其固有頻率處的峰值比較大，另一頻率處的峰值比較小；而在1：1共振時(shí)斜拉索和橋面兩個(gè)頻率點(diǎn)處的譜峰值均很大，這是因?yàn)榇藭r(shí)斜拉索和橋面的頻率近似相等。③共振情況下斜拉索和橋面的位移均呈現(xiàn)“拍”的特性。

 

2、參數(shù)影響分析

    2.1橋面激勵(lì)位移的影響

    通過(guò)改變橋面的初始激勵(lì)位移值來(lái)考察橋面激勵(lì)對(duì)斜拉索振幅的影響。計(jì)算中橋面初始位移值從0.005m變化到0.1m，計(jì)算結(jié)果見(jiàn)圖6。從圖6可以看出無(wú)論是非共振情況還是各種共振情況下，橋面的振幅則還是和其初始激勵(lì)值相同，而斜拉索的振幅均是隨著橋面初始位移激勵(lì)的增加而增加，而且接近于線性增長(zhǎng)關(guān)系。

 

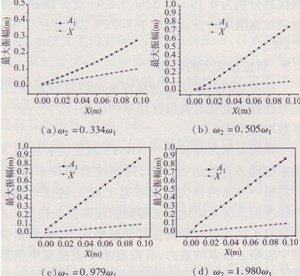
圖6斜拉索振幅隨橋面初始位移激勵(lì)的變化

    2.2斜拉索阻尼的影響

    考慮斜拉索阻尼時(shí)拉索的運(yùn)動(dòng)微分方程為：

  

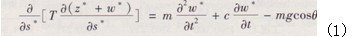
    式中：c為拉索的阻尼系數(shù)。采用和文獻(xiàn)[1]相同的處理方法，得到考慮斜拉索阻尼的系統(tǒng)運(yùn)動(dòng)微分方程為：

 

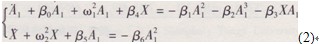
    式中：阮β0=c/m，其他系數(shù)同前。

    通過(guò)改變斜拉索的阻尼系數(shù)來(lái)考察斜拉索的阻尼對(duì)拉索振幅的影響。計(jì)算中斜拉索的阻尼系數(shù)從0.2 N·s/m變化到26 N·s/m，相應(yīng)的一階阻尼比在0.042％～5.5％的范圍內(nèi)。

    圖7所示為共振情況下及非共振情況下斜拉索最大振幅隨拉索阻尼系數(shù)的變化。由圖可見(jiàn)，隨著斜拉索阻尼系數(shù)的增加，斜拉索的最大振幅減小。對(duì)于頻率比為1：3、1：2以及2：1共振情況，當(dāng)拉索的阻尼系數(shù)分別達(dá)到3、2、6、11N·s/m(對(duì)應(yīng)的阻尼比分別為0.63％、0.42％、l.26％、2.2％)時(shí)，曲線的斜率明顯減小，即斜拉索阻尼的抑振作用減弱，分別見(jiàn)圖7中的曲線(a)、(b)及(c)。而對(duì)于l：1共振，斜拉索振幅隨阻尼變化曲線的斜率沒(méi)有明顯變化，見(jiàn)圖7中曲線(c)。

    在實(shí)際的斜拉橋中，斜拉索的阻尼比很小，典型的一階阻尼比值為0.16％，一階阻尼比不超過(guò)0.2％。圖7中，當(dāng)阻尼比為0．2％時(shí)，拉索最大共振位移分別為0.19m、0.52m、0.83m及0.78m，比不考慮斜拉索阻尼時(shí)分別減小了24.2％、24.0％、2.3％及9.2％。

    2.3斜拉索張力的影響

    在考察斜拉索張力對(duì)系統(tǒng)振動(dòng)特性的影響之前，先考察張力變化對(duì)斜拉索頻率的影響。5種計(jì)算工況參數(shù)取值見(jiàn)表l。

    采用有限元分析軟件ANSYS對(duì)上面各工況下斜拉索的動(dòng)力特性進(jìn)行計(jì)算，得到拉索的頻率和振型，并將第一階面內(nèi)模態(tài)的頻率列于表2，將這個(gè)結(jié)果作為標(biāo)準(zhǔn)值來(lái)衡量簡(jiǎn)化算法得到的頻率值的精度。表2中比較了本文中三種簡(jiǎn)化算法的結(jié)果，其中張緊弦模型中忽略了拉索的重力，有垂度水平索模型中雖然考慮了拉索的重力但卻忽略拉索重力沿索弦線方向的分力，而本節(jié)中的斜索模型對(duì)拉索重力垂度的簡(jiǎn)化最少，和實(shí)際拉索比較接近。

 

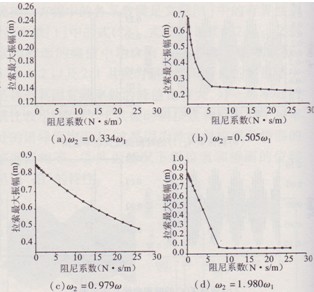
圖7斜拉索振幅隨拉索阻尼的變化

表1不同張力時(shí)索A20的基本參數(shù)

 

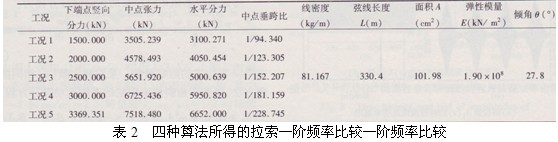
    圖8為不同索張力下系統(tǒng)的最大振幅隨頻率比的變化。由圖可見(jiàn)，隨著斜拉索張力的增大，各種共振情況下以及當(dāng)ω2/ω1<0．5時(shí)斜拉索最大振幅均減小，且共振區(qū)的寬度有所減小，各共振區(qū)峰值中心對(duì)應(yīng)的頻率比ω2/ω1分別向l/2、1和2逼近。圖9給出了斜拉索各共振區(qū)中心對(duì)應(yīng)的頻率比ω2/ω1。隨索張力的變化。由圖可見(jiàn)，斜拉索張力越小ω2/ω1相對(duì)于1/2、1和2的偏離值越大，其中ω2/ω1在1和2附近為向下偏離，ω2/ω1在1/2附近為向上偏離。這些偏離是由斜拉索的垂度引起的，這可從文獻(xiàn)[1]中共振條件的推導(dǎo)中看出。

 

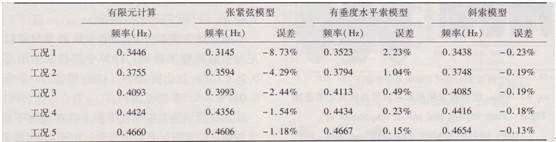
    圖8為不同索張力下系統(tǒng)的最大振幅隨頻率比的變化。由圖可見(jiàn)，隨著斜拉索張力的增大，各種共振情況下以及當(dāng)ω2/ω1<0．5時(shí)斜拉索最大振幅均減小，且共振區(qū)的寬度有所減小，各共振區(qū)峰值中心對(duì)應(yīng)的頻率比ω2/ω1分別向l/2、1和2逼近。圖9給出了斜拉索各共振區(qū)中心對(duì)應(yīng)的頻率比ω2/ω1。隨索張力的變化。由圖可見(jiàn)，斜拉索張力越小ω2/ω1相對(duì)于1/2、1和2的偏離值越大，其中ω2/ω1在1和2附近為向下偏離，ω2/ω1在1/2附近為向上偏離。這些偏離是由斜拉索的垂度引起的，這可從文獻(xiàn)[1]中共振條件的推導(dǎo)中看出。

 

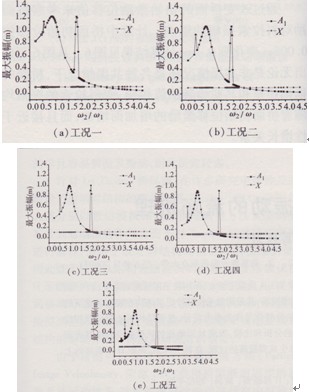
圖8不同索張力下斜拉索和橋面的最大振幅隨頻率比的變化

 

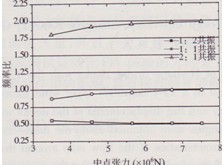
圖9斜拉索各共振區(qū)中心對(duì)應(yīng)的頻率比隨索張力的變化

3、結(jié)論

    本文基于《斜索一橋面耦合面內(nèi)參數(shù)振Ⅰ：理論模型》的理論模型，以南京二橋A20拉索為對(duì)象，用數(shù)值解對(duì)近似解析解的結(jié)果進(jìn)行驗(yàn)證，最后討論系統(tǒng)參數(shù)對(duì)索一橋耦合振動(dòng)響應(yīng)的影響，得到了以下結(jié)論：

    (1)隨著垂跨比的增大，應(yīng)考慮拉索垂度的影響以及拉索重力弦向分力的影響，以求得到較為精確的拉索一階頻率結(jié)果。

    (2)當(dāng)橋面和拉索一階頻率比接近1/3、1/2、1以及2時(shí)，系統(tǒng)發(fā)生內(nèi)共振。發(fā)生內(nèi)共振時(shí)，拉索的振幅遠(yuǎn)大于其初始擾動(dòng)，而橋面的振幅基本上和其初始位移相同，但兩者均呈現(xiàn)拍的振動(dòng)特性。在共振情況下，即使不考慮拉索和橋面的阻尼，系統(tǒng)的振幅也都滿足有界性條件，是有界量。

    (3)拉索一階響應(yīng)以及橋面的響應(yīng)成分中均兩個(gè)頻率成分，但以各自固有頻率為主。

    (4)隨著拉索張力增大，拉索垂跨比減小，系統(tǒng)1：2、1：1及2：1內(nèi)共振區(qū)中心對(duì)應(yīng)的頻率比分別以0.5、1和2為漸近線；且拉索的振幅減小，l：1內(nèi)共振時(shí)的共振區(qū)寬度減小。

    (5)初始激勵(lì)對(duì)拉索的振幅有較大影響，拉索的振幅隨著橋面初始位移激勵(lì)的增加而線性增大。

    (6)隨拉索阻尼比的增加，拉索的振幅減小。

參考文獻(xiàn)

[1]任淑琰，顧明．斜索一橋面耦合面內(nèi)參數(shù)振動(dòng)l：理論模型[J]．土木工程學(xué)報(bào)，2009，42(5)：79—84

[2]同濟(jì)大學(xué)計(jì)算數(shù)學(xué)教研室．?dāng)?shù)值分析基礎(chǔ)[M]．上海：聞濟(jì)大學(xué)出版社，l998   

[3]任淑琰．斜拉橋拉索參數(shù)振動(dòng)研究[D]．上海：同濟(jì)大學(xué)，2007

(本文來(lái)源：陜西省土木建筑學(xué)會(huì)  文徑網(wǎng)絡(luò)：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)

上一篇： 南水北調(diào)工程工期影響因素的問(wèn)卷調(diào)查及分析

下一篇： 活性粉末混凝土低高度梁設(shè)計(jì)及試驗(yàn)研究