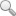陜西土木建筑網首頁 > 學術研究 > 課題研究 > 地基非線性沉降計算的原狀土割線模量法

摘要：地基的沉降計算如何較準確而又簡便是工程實踐中一直未很好解決的問題。為較好解決地基沉降計算這一重要難題，提出一種原狀土割線模量法，就是利用原狀土的壓板試驗曲線，假定壓板試驗曲線符合雙曲線方程，利用Bussinesq解，建立不同荷載水平下土體的等效割線模量。對于實際基礎，則根據土體不同深度的應力水平，從壓板試驗曲線確定原狀土的割線模量，然后用于分層總和法進行地基非線性沉降計算，通過試驗曲線的驗證和實際工程的應用，證明該方法效果較好，可較準確計算地基的沉降。...

地基非線性沉降計算的原狀土割線模量法

楊光華  王鵬華  喬有梁

1. 廣東省水利水電科學研究院，廣東廣州510610； 2．華南理工大學， 廣東廣州510640

前言

    基礎沉降計算是土力學中古老而目前還并未很好解決的問題，以致目前一般規范的沉降計算還采用差異變化較大的經驗系數進行修正，如國家健筑地基基礎設計規范》GB50007～2002)采用壓縮模量分層總和法，沉降計算經驗系數ms=0.2～1.4。究其原因，其中影響較大的應主要是計算參數的確定，因一般沉降計算的參數，如壓縮模量，主要是通過取樣進行室內試驗來測定，而天然土一般具有結構性，尤其是硬土，取樣后室內試驗與原狀土參數差異很大，如廣東普遍存在的粉質黏土、花崗巖殘積土等，原位壓板試驗確定的變形模量是壓縮模量Esl-2的6～10倍，一般Es=4～10MPa，而變形模量Eo=30～60MPa，與兩者之間理論值相差甚遠且相反，因而一般硬土的經驗修正系數小于1；而對于軟土，則由于壓縮模量不能反映側向變形產生的沉降，其經驗系數則一般大于l，且國內不同規范，軟土的沉降經驗系數也不同，如《堤防工程設計規范》(GB50286—98)，ms=1.3～1.6，《建筑地基處理技術規范》(JGJ79-2002)ms=1.1～1.4，《公路橋涵地基與基礎設計規范》既(JTJ24—85)則當 Es=1～4MPa時，取ms=1.1～1.8。因此，作為地基沉降計算的準確性，主要受土性參數的合理確定和土的變形特性影響。

    這兩個因素，即使是采用彈塑性本構模型和有限元數值方法等現代土力學理論，也較難解決土體結構性對參數的影響，且計算復雜。因此，一個好的計算方法，應要較好地解決以上兩個因素的影響而又簡單實用。作者提出利用壓板試驗曲線，引入類似Duncan—Chang本構模型中的應力水平系數的原狀土切線模量法，在較好程度上解決地基沉降計算中的難題，取得較好的效果，是目前一些規范方法利用變形模量法和弦線模量法的進一步發展。切線模法是采用增量逐級計算，不能直接計算某一荷載下的沉降，為此，本文發展一個原狀土割線模量法，可以一次計算不同荷載的沉降量，相當于是全量法，而原狀土切線模量法則相當于增量法。

一、 原狀土割線模量法

    1.1原狀土割線模量分層總和法

    分層總和法簡單方便，能考慮層狀分布的特點，是目前較為簡捷的沉降計算方法，但缺點是參數通常采用壓縮模Es，或變形模量Eo，但Eo應是與應力水平有關的，不同深度處不同點，土體的應力水平是不同的，因此，Eo也是變化的，合理取值應按不同應力水平取其割線模量，則不同深度處不同土層，該處相應應力水平設為β=pi／pui，相應β值的割線模量為Eo，基礎荷載P0作用在hi深度處產生的豎向應力為pi ，pi=αp0，α為應力分布系數，可按彈性解近似確定，P0為基礎底面作用于土層上的分布荷載，如圖l所示，Pui為深度hi處相應基礎的土層極限承載力，則hi處土層厚度為Δhi引起的沉降增量為：

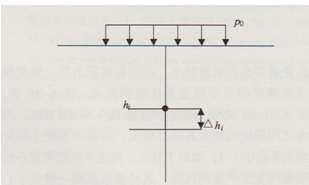
圖1 hi深度處厚度Δhi引起的沉降量

    則P0荷載下某點沉降量為

    因此，這種方法其實是在分層總和法中土的變形參數采用了原狀土的割線模量Eβo。

    1．2原狀土割線模量的確定

    為簡便，可把原狀土體的壓板試驗的荷載沉降 p-s設為一雙曲線方程

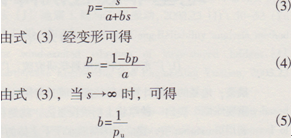
    Pu為壓板試驗時的極限荷載，可知，曲線的初始切線模量α為

    式中：μ為土的泊松比；ω為幾何參數；E。為原狀土的初始切線模量。

    式(3)為壓板試驗的p-s曲線，相當于一個邊值問題，我們要利用該邊值反求土體的參數。假設某一荷載p作用下，土體的等效割線模量Ep在土體等效割線模量下按線性考慮，如圖2所示，則此時對應的壓板沉降可由Bussiuesq解求出為：

 

圖2 P荷載作用下土體的等效割線模量E。

    若考慮Pu值離真正極限值是偏小的，則可以像 Duncan．Chang模型一樣，引入一應力水平修正系數 Rf≤l，即取

    則Ep可理解為壓板底處土體的等效割線模量。    

    當采用分層總和法時，不同深度hi處相應的應力P可由彈性解求得，而Pu則要考慮相應埋深的影響，隨著埋深hi的增大，顯然P會隨之減少，Pu會增大，因而Ep會隨hi的增大而增大。

二、應用和驗證

    采用工程實例檢驗方法的可行性。

    2.1方法的驗證

    為檢驗割線模量方法，首先對壓板試驗進行驗證，即利用壓板試驗曲線按以上公式求割線模量，利用所求得的割模量用分層總和法求出不同荷載下壓板的沉降值，與試驗結果進行比較，以驗證方法的可行性，然后進一步應用于一個筏板基礎工程，并與實測值進行比較。圖3所示為某筏形基礎基底面高程進行的三個壓板試驗所得的p-s曲線，壓板直徑為D=80cm的圓形壓板，以3#試驗點的曲線來確定其割線模量。

 

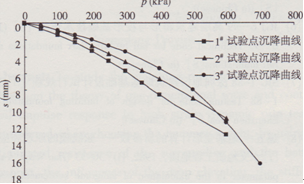
圖3三個試驗點的壓板載荷試驗p.s曲線

    對式(1)可改寫為

 

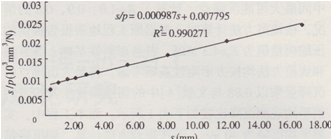
圖4 3#試驗點s／p-s關系線

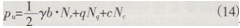
    根據Prandtl地基承載力公式，假設φ=25°，可以反算土的C值N，=15.2，NP=l0.7，Nc=20.7，γ=20kPa，b=0.8 m，q=0。   

    把pu=1000 kPa代人式(14)，則可得c=42.4 kPa，對于不同深度處，p值按圓形荷載下彈性應力分布求得，pu按c，φ值用式(14)考慮埋深時q=γh的影響而可求得，分層土層厚度取為0.5 m，按式(10)確定不同深度處土體的割線模量，按分層總和法僅考慮豎向應力引起的沉降。對3#試驗點，割線模量法、切線模量法=4]計算沉降與試驗沉降曲線進行比較如圖5所示。由圖可見，計算與實測值是接近的，且可以計算荷載直至接近破壞的全沉降過程，可以反映非線性的沉降過程，從3”試驗點求得的參數用于3#點的計算上看，計算值略大于實測值，說明方法也是偏安全的。

 

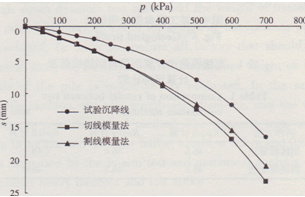
圖5 Rf-1．0時兩種方法計算沉降與實測沉降比較

    2．2工程應用

    該工程典型地質剖面如圖6所示，基坑開挖深度約l2 m，建筑物地面以上l2層，地下室2層，采用以上的割線模量法和所求得的有關參數，對該工程的筏板基礎沉降進行計算，基礎面積近似按40m×40 m方形考慮，實際基底應力按每層l5kPa，按l4層考慮，則按p=210 kPa計算沉降，按分層總和法計算，分層厚度按1m考慮，計算深度至基礎底以下20m，20m以下為強風化巖面，巖層的沉降不計。對筏板中間最大可能沉降點，計算了Rf=1.0、0．9、0．8的情況，按規范方法計算時，根據原工程地質報告提供的壓縮模量值為Es=4．3 MPa，若考慮剛性基礎，新方法和規范方法均按方形剛性基礎考慮，將最大沉降點的沉降量乘以0．88與文獻中的切線模量法及竣工時的平均觀測沉降比較如下表l所示。而本工程中，實測平均沉降為40mm，若按規范方法計算，則沉降量774.3mm。由以上計算結果可見，用這種新方法計算的沉降量與切線模量法及實測結果較接近，而用壓縮模量Es，按規范的分層總和法計算的沉降則明顯偏大很多，說明新方法是符合實際的。

 

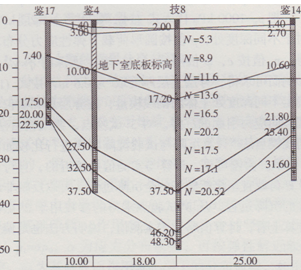
圖6某工程典型地質剖面

表1割線模量法計算沉降與切線模量法

    計算沉降比較

三、結論

    根據原狀土的壓板試驗曲線和應力水平狀態來確定土的變形計算參數，可以較好解決前面所指出的目前地基沉降計算中的難題，即土體結構性和應力狀態所產生的非線性，按原狀土試驗曲線確定的隨應力水平而變化的割線模量參數進一步用于分層總和法計算可以得到較好的效果，方法簡便，便于工程應用，且具有較高準確性和可以計算基礎非線性沉降的全過程，其與切線模量法一樣，相信對于解決地基沉降計算是一個較有發展前途的方法，切線模量法需按增量法計算，而割線模量法可直接計算某一級荷載下的沉降，相當于全量法，故更為簡便。

參考文獻

[1] GB50007--2002建筑地基基礎設計規范[s]『2]GB50286---98堤防工程設計規范[s](GB50286---98 Code  for design of levee project[S](in Chinese))

[3]JTJ024--85公路橋涵地基與基礎設計規范[s]

[4]楊光華．地基非線性沉降計算的原狀土切線模量法[J]巖土工程學報，2006，(11)：1927-1931

[5]DBJ l5—31—2003建筑地基基礎設計規范[S]

[6]JGJ 6—99高層建筑箱形與筏形基礎技術規范[S]

[7]SJG l-88深圳地區建筑地基基礎設計試行規程[S]

[8]焦五一．地基變形計算的新參數——弦線模的原理和應用[J]冰文地質工程地質，1982，(1)：30—33

[9]楊光華．殘積土上基礎非線性沉降的雙曲線模型的研究[C]／／第七屆全國巖土力學數值分析與解析方法討論會論文集．大連：大連理工大學出版社，2001：168—171

[10]楊光華．基礎非線性沉降的雙曲線模型法[J_．地基處理，1997，(1)：50—53

(本文來源：陜西省土木建筑學會     文徑網絡：呂琳琳  尹維維 編輯   文徑 審核)

上一篇： 超高強微鋼纖維增韌混凝土的制備及其力學性能研究

下一篇： 不同角色視角的建筑施工項目關鍵因素實證分析