陜西土木建筑網首頁 > 學術研究 > 課題研究 > 天然軟黏土屈服面及流動法則試驗研究

摘要：天然沉積的軟黏土往往具有結構性和塑性各向異性，通過對K0固結溫州軟黏土的l9組三軸排水應力路徑試驗和4組三軸不排水剪切試驗的研究，揭示典型結構性軟黏土的屈服特性和屈服后的塑性流動特征。...

天然軟黏土屈服面及流動法則試驗研究

沈愷倫　王立忠

浙江浙峰工程咨詢有限公司　浙江杭州310012　浙江大學　浙江杭州310027

引言

    早期臨界狀態土力學本構模型建立在各向等壓固結重塑土的三軸試驗基礎上，理論上通常假定塑性各向同性，因此屈服面關于P軸對稱分布，如原始劍橋模型和修正劍橋模型。隨著人們對天然狀態軟黏土結構性及各向異性認識的不斷深入和室內三軸試驗條件的逐步改善，采用更符合天然土體的屈服面，正日益成為國內外軟黏土塑性性狀研究的一個重點。在天然軟黏土屈服面的數學描述方面，有學者認為P ′一q應力平面上屈服面大致關于K0同結線對稱，另一些學者在原始劍橋模型屈服面的的基礎上，通過將子彈頭形屈服面旋轉至子彈頭尖點位于瓦線上，從而得到各向異性天然土體屈服面，如 Ohta等 (1985)采用的本構模型。還有一些學者通過旋轉修正劍橋模型的橢圓屈服面得到K0固結軟黏土的屈服面，其中的一些做法與Ohta等的方法相似，將橢圓旋轉至橢圓的右切點位于K線上，如 Nakan0等 (2005)的模型；另一些做法則認為橢圓傾斜的程度要小一些，橢圓右切點位于K0線和P′軸之間的某一位置，如Wheeler等(2003)的模型；作者也曾采用Wheeler建議的屈服面考慮軟土結構性對天然軟黏土本構關系進行研究。為進一步了解天然軟黏土的屈服性狀以及屈服后的塑性流動特性，本文選取溫州軟黏土進行了三軸試驗研究。

    本文在k0固結試驗的基礎上進行三軸應力路徑試驗，獲得了結構性軟黏土的初始屈服面，并通過進一步收集并重新整理各種天然軟黏土的試驗資料，選取了一個適合于k0固結結構性軟黏土的屈服面方程。其次，在擬采用上述K0固結溫州軟黏土屈服面的前提下，通過描繪屈服后土體塑性流動方向和定量分析該流動方向與屈服面法線方向的偏離程度，進一步整理其他各種天然軟黏土的試驗資料，評價相關聯流動法則對于K0固結結構性軟黏土的適用性。最后，通過對繇固結的溫州軟黏土施加一個較大的等向應力進行進一步固結，然后進行各種應力路徑的三軸試驗，分析評價屈服面的旋轉硬化特性和屈服面旋轉后的塑性流動性狀。

1、溫州軟黏土基本性狀

    王立忠等 (2002，2004)曾對溫州軟黏土的基本物理性質和一維壓縮特性作了系統的研究，其取土位置位于甌江入海口處的溫州發電廠二期工程的2#、3#煤場，原狀土取土采用不銹鋼管的薄壁取土器。該處淤泥層厚度約為27m，層頂距離地表1.5m左右。試驗結果表明，溫州軟黏土5～15m深度范圍內的淤泥層具有明顯的結構性，隨著深度增加，含水量和孔隙比逐漸減小，結構性逐漸減弱。現場3組十字板試驗表明溫州軟黏土的靈敏度沿深度分布離散性不大，大部分深度范圍內St在3～6之間，3組試驗在5～15 m深度范圍內St的平均值為4.54。而在15m以下，淤泥層軟黏土的靈敏度急劇下降，軟黏土的結構性不斷降低，因此研究溫州軟黏土的結構性最好選取最具有代表性的5～15m深度范圍內的淤泥層。

    本次試驗的取土位置位于溫州城區溫州火車站附近的華盟廣場項目的基坑工地，取土深度為地表下11m。地質報告提供的淤泥層平均含水量為64.3％，本次試驗所取llm深度處土體的含水量(取3組土樣平均)為68.4％，略高于平均值；界限含水量測試采用液塑限聯合測定儀測定，試驗結果離散性較小，其中液限ωI=63.4％，塑限ωp=27.6％，塑性指數Ip=35.8％，液性指數IL=1.14。靈敏度試驗采用原狀土和重塑土的無側限抗壓強度試驗得到，試驗結果表明溫州軟黏土靈敏度為St=5．45，略高于前述溫州煤場現場十字板試驗5～15 m平均St=4．54的結果。其余常規物理力學試驗結果為：天然孔隙比e0=1．916，天然密度P0=1．588 g/cm³，顆粒相對密度Gs=2.75，壓縮模量Esl-2 =1.35 MPa，滲透系數Kh=5.9×10-6cm/s，Kv=2.4×10-6cm/s。

    溫州軟黏土的有效強度參數由常規等向固結三軸不排水試驗(CIU)確定。試驗將四組土樣分別等向同結到50kPa、100kPa、150kPa和300kPa然后施加豎向應力，試驗所得不同圍壓下的有效應力路徑及其臨界強度和峰值強度的擬合直線。其中臨界強度對應主應力比最大值(σ′1／σ′3)max的試驗點，峰值強度則對應主應力差最大值(σ′1-σ′3) max的試驗點。試驗結果表明臨界強度擬合線總在峰值強度擬合線上方，由兩者斜率計算得到的臨界強度有效內摩擦角略大于峰值強度有效內摩擦角，但其偏差均不超過1°。試驗得臨界狀態強度參數為c ′= 8.4kPa，φ′=25.4°；若限定擬合的臨界狀態線CSL過應力原點，得臨界狀態強度參數為φ′=28.80，M=1.146。

2、試樣情況與試驗內容

    本次取土平面位置在基坑范圍內工程樁稀疏的區域，且工程樁均為泥漿護壁的鉆孔灌注樁，對土體擾動相對較小。當基坑開挖到llm深度時用不銹鋼薄壁取土盒(25cm×25cm×20cm，壁厚0.8mm)切取塊狀土樣，如圖1所示，其擾動程度小于不銹鋼管薄壁取土器所取的土樣。為確保所取土樣盡可能保持原狀，根據llm以上各層土體的有效重度及其厚度，計算得原位豎向有效應力為σ′v0 =75.4kPa。三軸試樣高度為76mm，直徑38mm。根據Bothkennar軟黏土試驗研究得出的結論，用鋼絲鋸切取土樣對保持土樣的原狀特性最為有效。本文試驗研究在制樣時采用鋼絲鋸，并盡可能切取塊狀土的中心部位，以盡量避免表面局部干燥對土樣的影響．

 

圖1  試驗取土裝置和土樣斷面照片

    試驗制備中發現，多數土樣斷面呈現青灰色土體和黃褐色土體交錯的現象，但都呈現出典型的淤泥質土體的特性。大部分塊狀土樣較為均勻且完整，并含有少量粉砂質夾層，但鮮有貫通整個土樣的夾層出現。夾層和雜質的存在對土樣的試驗結果有較大的影響，尤其是對拉伸試驗，因此本文試驗過程在制樣時盡可能避免三軸試樣含有粉砂夾層等雜質，以更好地體現淤泥的特性。試驗采用的主要試驗設備為GDS應力路徑三軸試驗系統。在進行％固結試驗時，該系統通過反壓控制器測得的試樣體變反算試樣平均斷面積，不斷調整軸向應力和側向應力以保持試樣直徑不變即試樣無側向應變。本文對溫州軟黏土屈服性狀試驗研究的主要內容為：

    (1)K0同固結試驗：考察軟黏土的一維固結壓縮情況，確定％固結系數，為后續試驗提供試驗參數，并用以確定屈服應力比YSR等參數。試驗起始先給試樣施加一個較小的圍壓和軸壓，軸壓控制在10kPa，圍壓根據預估K系數設置為5 kPa；然后連續一維加壓至豎向應力到達290kPa(11m深度處原位豎向有效應力75.4kPa)，該過程歷時67h；然后進行一維卸載，該過程歷時48h。

    (2)K0固結應力路徑三軸試驗：沿不同應力路徑，分別進行三軸壓縮和拉伸試驗，用以研究溫州軟黏土的應力應變關系、屈服面的特征和屈服后的塑性流動性狀。根據以上K0固結試驗得到的K0系數和11m深度處的原位豎向有效應力75．4 kPa，計算得原位水平向有效應力為41.5kPa。K0固結三軸應力路徑試驗首先將土樣逐步固結到原位應力狀態(σ′v0 = 75.4kPa，P′0 = 52.8kPa)，然后沿不同直線應力路徑加載，加載速率為4kPa/h，直至試件破壞或到達人為設定的應變界限值。應力路徑試驗均為排水條件，所設路徑如圖2(a)所示。圖中應力路徑符號意義為：B表示塊狀土樣，CD表示排水壓縮  試驗，ED表示排水拉伸試驗，BCD或BED后數字表示直線應力路徑在P′一q平面上與水平方向的傾角，以逆時針為正。此外還進行了兩組不排水試驗，剪切速率為0.065％/min，下文以BCU和BEU表示。

    (3)為了進一步考察結構屈服面在加載過程中的旋轉性狀，本文在上述排水三軸試驗確定初始屈服面的基礎上，設計了一組特定的旋轉硬化應力路徑三軸試驗。試驗過程為：首先如K0固結應力路徑三軸試驗系列試驗一樣固結到原位應力，然后逐步加載到等向固結應力狀態(P′0= 160kPa≈3p′0，q1=0，可認為結構性已破壞嚴重)，再緩慢卸載到此前應力的一半(P′2 =80kPa，q2=0)，最后沿不同應力路徑進行加載。該組試驗固結一卸載一加載的應力路徑如圖2(b)所示，圖中BRCD和BRED分別表示排水三軸試驗的有效應力路徑，其后數字表示應力路徑和p ′軸的夾角。此外還進行了兩組不排水試驗，下文以BRCU和BREU表示。

 

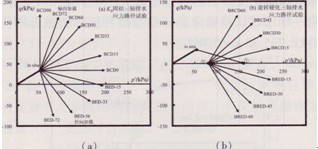
圖2溫州軟黏三軸排水試驗應力路徑

3、試驗成果

    (1)K0固結試驗成果

    K0固結試驗目的之一是確定K0系數，試驗全過程的K0值(水平向與豎向有效應力比)隨豎向有效應力的變化過程如圖3所示。根據王立忠等(2006)的觀點，結構性軟黏土原位土體的K0系數應取加載過程中屈服后結構性接近完全破壞后的數值。圖3所示溫州軟黏土礫固結試驗在豎向有效應力大于150kPa后逐漸趨向穩定，本次試驗取值為K00.55。

 

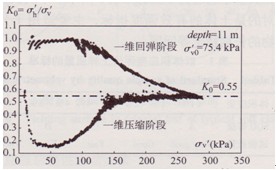
圖3溫州軟黏土的K0系數

     K0固結試驗的另一個目的是考察溫州軟黏土的一維壓縮性狀，e～logσ′v。平面中其一維壓縮回彈曲線如圖4所示。可見，溫州軟黏土一維壓縮試驗表現出明顯的分段特性，是典型的結構性軟黏土的特征。壓縮指數可由壓縮曲線最后直線段斜率獲得，回彈指數由回彈線斜率獲得，其值分別如圖4所示。豎向屈服應力對應壓縮曲線曲率最大點為l20kPa左右．其與原位應力(75.4kPa)的比值為屈服應力比，得YSR=1.6。天然軟黏土一維壓縮曲線的最后一個直線段軟黏土結構破壞程度較大，該直線段斜率與重塑土的一維壓縮線斜率接近，通常可用來近似確定重塑土的壓縮系數指數λ；而相應的回彈曲線也可用來近似確定重塑土的回彈指數ko對于溫州軟黏土，由一維壓縮試驗確定的壓縮指數和回彈指數分別為λ=0.345和，k=0.051。

 

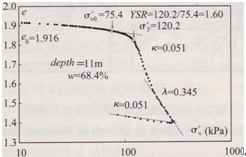
圖4溫州軟黏土的一維壓縮曲線

    此外，可根據K0固結試驗過程中有效豎向應力與土體原位有效豎向應力相同時的體積應變大小對土樣的質量進行評價。根據Terzaghi等(1996)的方法，土樣質量可分為如表1所示5個SQD等級。溫州軟黏土K0固結試驗過程中有效豎向應力為原位有效豎向應力，即σ′V75.4kPa時，試樣體積應變為1.54％，SQD等級為B，試樣質量較好。通過本文溫州軟黏土試驗結合以往對溫州軟黏土的試驗研究，其基本物理力學指標如表2所示。本次試驗分析針對的是土體的有效強度指標，主要適用于分析結構物的長期穩定等問題。

表1  以體積應變評價土樣質量的標準

表2溫州軟黏土常規物理力學指標

 

    (2)K0固結三軸應力路徑試驗成果

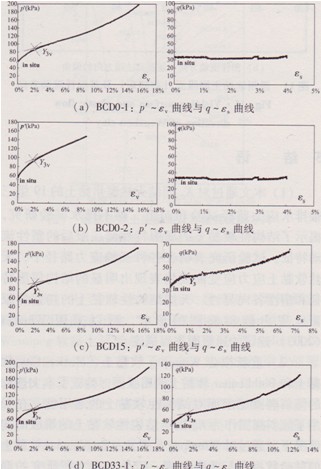
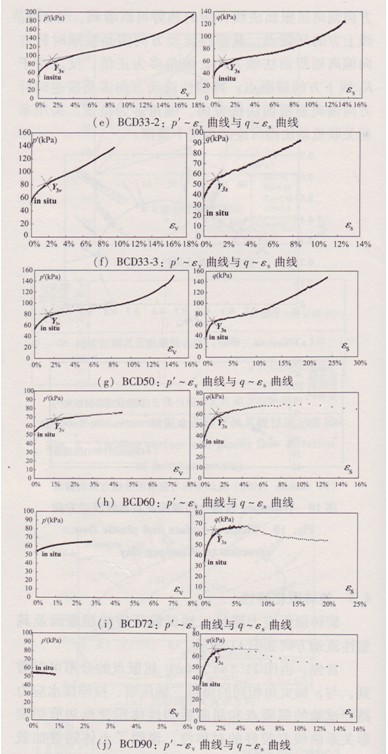
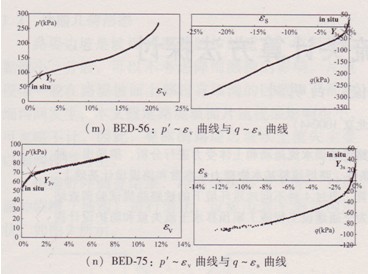
    K0固結三軸應力路徑試驗各種應力路徑下的應力應變曲線(P′-εv曲線和q—εs曲線)如附錄A所示，BCD系列為三軸壓縮試驗，BED系列為三軸拉伸試驗。各種應力路徑下應力應變曲線表明，溫州軟黏土有明顯的結構屈服的特征，各種應力路徑試驗得到的屈服點用Y3v或Y3s。表示于圖中，insitu表示天然固結應力狀態，即應力路徑試驗加載的起始點。屈服點的確定在參考Bothkennar軟黏土試驗研究方法的基礎上，將屈服前后直線段延伸線的交點向試驗曲線作垂直線獲得的曲率最大點確定為屈服點。

    三軸不排水壓縮和拉伸試驗的應力路徑和剪切應力應變曲線如圖5所示。圖5(a)所示K0固結三軸不排水壓縮試驗和拉伸試驗的總應力路徑和有效應力路徑中，TSP表示總應力路徑，ESP表示有效應力路徑。不排水試驗的屈服點由試驗的剪應力剪應  變曲線的曲率最大點確定，圖中以Y3表示，由該應力應變曲線可見，正常固結的溫州軟黏土有明顯的應變軟化現象，表現出了明顯的結構性軟黏土特征。最后將這些屈服應力點描繪在應力平面上，即可得到部分的初始屈服面幾何形狀。

 

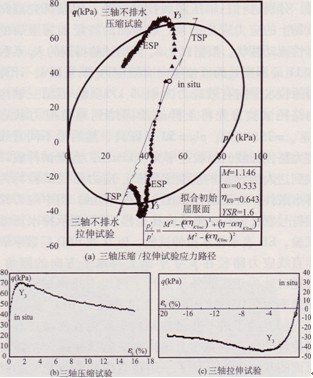
圖5溫州軟黏土三軸不排水試驗應力路徑和應力應變曲線

4、試驗結果及分析

    4.1初始屈服面形狀

    關于K0固結軟土屈服面在P′一q平面上近似為傾斜橢圓的事實已為大量的室內試驗所證實(Graham等，1983)，本文考慮了K0固結誘發的各向異性的影響采用了傾斜橢圓形來擬合結構性軟黏土的屈服面，并通過收集一些典型軟黏土的試驗資料以及溫州軟黏土的試驗成果揭示了擬合屈服面的合理性。近年來，國內外文獻中報道的關于p′-q平面上橢圓  屈服面的形狀大致可分為以下三種：修正劍橋模型的水平橢圓屈服面、Nakan0等(2005)模型所采用的傾斜橢圓屈服面和本文采用的Wheeler等(2003)提出的傾斜橢圓屈服面，其橢圓方程分別如式(1)、式(2)、式(3)所示：

 

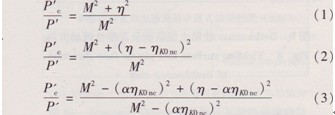
    式(1)～式(3)中P′c表征了橢圓屈服面的大小，叩ηK0nc為％固結對應的應力比，α表征了正常固結線NCL傾角大小，其初始值為α0。式(1)所示屈服面是關于等向固結線P′軸對稱的，即正常固結線NCL與P′軸重合；而式(2)和式(3)屈服面的NCL則與P ′軸均有一傾角，對于初始屈服面，該傾角的正切值分別為ηK0nc和α0ηK0nc。本文采用的屈服面式(3)的傾斜程度即NCL斜率的大小由α控制，根據Wheeler等(2003)的分析，由模型一維壓縮條件下的體積應變和剪切應變的比例關系，可推導出其初始值d。為：

 

    對于常見范圍內的軟土，Wheeler等指出α0的取值范圍為0.58～0.7。因此，只要獲得了K0值(可換算得ηK0nc值)和M值，初始屈服面的形狀便確定了；而初始屈服面的大小則由初始結構性大小決定，反映在屈服面方程上即為P ′初始值P ′c0和P′c的比值，可近似由屈服應力比YSR確定。

    圖6所示為文獻中試驗得到的3種典型軟黏土的屈服點和本文模擬的初始屈服面，圖7(a)所示為本文溫州軟黏土K0固結三軸應力路徑試驗得到的屈服點和本文模擬的初始屈服面，可見這4種土的初始屈服面形狀近似為一個傾斜的橢圓，并且斜率為α0ηK0nc的直線與橢圓的兩個交點近似為其豎向切點，說明本文采用的屈服面方程是合理的，能很好地擬合試驗結果。同時不難發現，當初始應力比ηK0nc較小時，K0線與橢圓的兩個交點也可近似認為是其豎向切點，此時K0線與NCL較為接近(如Winnipeg黏土)，用式(2)或式(3)擬合差別不大；但當初始應力比ηK0nc較大時， K0線與NCL的距離較遠(如Bothkennar黏土、Mexico City黏土和溫州黏土)，用式(3)擬合結果更合理。可見對于大多數結構性軟黏土而言，本文的屈服面方程式(3)更加符合實際。

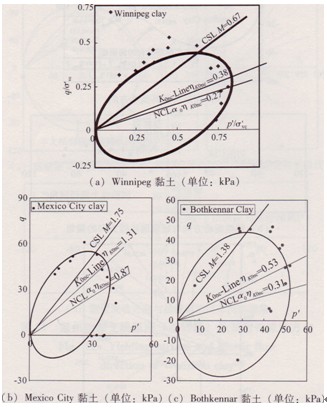
圖6  典型軟黏土三軸試驗屈服面

    4.2屈服后塑性流動性狀

    為了驗證正交流動法則的適用性，本文試驗將屈服點處的塑性應變增量方向也表示在圖7(a)中(應力應變共軸)，以短直線表示。在繪制屈服后塑性流動方向時，若所取應變量增值較小會造成數據的離散性較大，若取值較大則又不能反映屈服時的塑性流動方向。根據圖7(C)中屈服后各應力路徑試驗體積應變和剪切應變關系曲線可以看出，應變增量的矢量長度(約等于圖中曲線段長度)為1％時對應的應變增長方向基本可以代表屈服時刻的塑性應變方向，同時經歷的試驗點足夠多，可以較好避免試驗誤差。由溫州軟黏土屈服時的塑性應變方向和屈服面的相互關系可見，大部分應變方向垂直于屈服面切線方向，塑性應變方向與屈服面法線的夾角在-11°～l5°范圍之內，如圖7(b)所示(以順時針偏轉為正)，說明相關聯流動法則對于傾斜的橢圓屈服面是適用的。

 

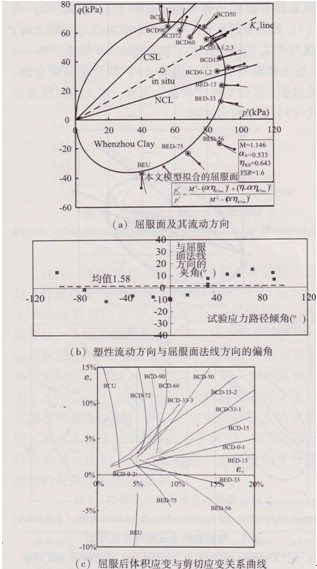
圖7溫州軟黏土屈服面及其塑性流動方向

    此外，為了進一步驗證相關聯流動法則對傾斜橢圓屈服面的適用性，本文還對Bothkennar軟黏土和 Winnipeg軟黏土試驗結果，用式(3)Wheeler建議的屈服面對試驗點進行了擬合，其對比結果及屈服后塑性流動方向如圖8和圖9所示。由Bothkennar軟黏土屈服時的塑性應變方向和屈服面的相互關系可見，大部分應變方向垂直于屈服面切線方向，塑性應變方向與屈服面法線的夾角Bothkennar軟黏土在-21°～l3°范圍之內，而Winnipeg軟黏土在-37°～23°范圍之內，波動相對較大。

 

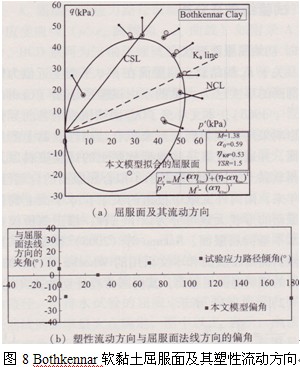
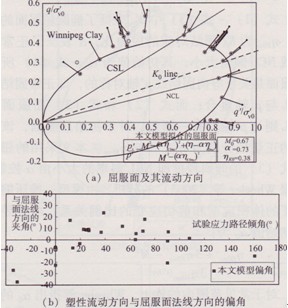
圖9 Winnipeg軟黏土屈服面及其塑性流動方向

    圖10為Graham(1983)對Winnipeg軟黏土屈服面的直接擬合以及塑性流動方向的驗證結果，相應偏角的波動范圍和本文選取的模型一樣相對較大。但總體上可以認為相關聯流動法則對于這兩種典型的軟黏土是適用的。此外，從三種軟黏土塑性應變方向偏離屈服面法線方向的趨勢可以看到，對于K0線上方的屈服點，其塑性流動方向多是按順時針方向偏離屈服面法線方向，偏角多為正值；反之對于 K0線下方的屈服點，其塑性流動方向多是按逆時針方向偏離屈服面法線方向，偏角多為負值。采用非相關聯流動法則時應注意這個規律。

 

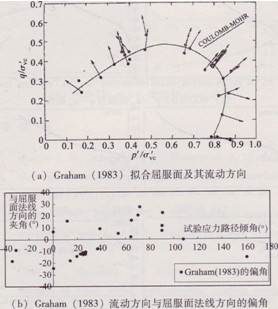
圖10 Winnipeg軟黏土屈服面及其塑性流動方向

    4.3旋轉硬化特性

    旋轉硬化應力路徑三軸試驗所得的屈服面及其塑性流動方向如圖ll所示。

    首先，由圖11(a)、(C)屈服點的分布可以看到，與P′軸夾角相同的每組三軸壓縮、拉伸排水應力路徑試驗的屈服點和屈服后塑性體積變形和剪切變形關系曲線有較好的對稱性，說明了土體隨著加載進行逐漸表現出各向同性的性狀。其次，由圖ll(a)屈服點處塑性流動方向與本文屈服面(實線橢圓，0 =0，P′c  =160kPa)法線方向基本一致，其偏角如圖11(b)所示，除三軸不排水壓縮試驗(BRCU)外均在-11°～6°范圍之內，小于初始屈服面的相應偏角(-11°～l5°)，說明隨著各項異性的喪失，塑性流動正交性也有所改善。此外，由圖11(a)可見，試驗屈服點多數落在式(3)對應屈服面之內，并有很好的規律性，隨著應力路徑傾角的加大，屈服點距離理論屈服面越遠。結合圖8(a)溫州軟黏土的初始屈服面試驗結果，初始屈服面對應的M=1．15對于旋轉后的屈服面是偏大的，屈服面擬合結果顯示，當取M=1.0時式(3)對應屈服面與試驗點的擬合結果更好，同時其正交性也更好。試驗結果表明，足夠大的等向應力可以使結構性軟黏土的塑性各向異性基本消失，土體在該應力作用過后發生較大的體積變形，逐漸呈現出塑性各向同性的力學性狀；在本文理論體系中，本次試驗旋轉后的屈服面為水平橢圓，即各向異性參數α由初始值α0 逐漸減小到零；隨著屈服面的旋轉和結構性的喪失，軟黏土的摩擦強度參數M有逐漸降低的趨勢，但降低幅度不大，采用M值恒定的假設帶來的誤差并不明顯。

 

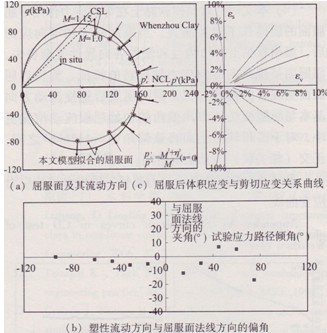
圖11溫州軟黏土屈服面(旋轉后)及其塑性流動方向

    州軟黏土的試驗結果分析表明，結構性軟黏土初始屈服后塑性流動方向基本與初始屈服面法線方向偏角不大，對于溫州軟黏土而言該偏角在-11°～l5°之間。因而，就結構性軟黏土而言，正交(相關聯)流動法則是基本適用的。

    (3)對天然軟黏土若采用非相關聯流動法則時應注意：在p′-q應力平面上，對于K0線上方的屈服點，其塑性流動方向是按順時針方向偏離屈服面法線方向；反之，對于K0線下方的屈服點，其塑性流動方向是按逆時針方向偏離屈服面法線方向。

    (4)本文同時對溫州軟黏土在等向應力作用下屈服面的旋轉作了試驗研究。當施加較大的等向應力后，溫州軟黏土的結構性和塑性各向異性逐漸喪失，屈服面呈現出向等向應力軸旋轉的特征。旋轉后屈服面呈現各向同性特征，同時屈服后塑性流動方向基本與屈服面法線方向偏角較初始屈服流動情況更小，對于溫州軟黏土而言該偏角在-11°～6°之間，正交(相關聯)流動法則適用。

    附錄A：溫州軟黏土應力路徑三軸排水試驗應力應變曲線

 

參考文獻

[1]王立忠，沈愷倫．K。固結結構性軟黏土的本構模型[J]．巖土工程學報，2007，29(4)：496-504

[2]王立忠，李玲玲，丁利，等．溫州煤場軟土結構性試驗研究[J]．土木工程學報，2002，35(1)：88—92

[3]王立忠，丁利，陳云敏，等．結構性軟土壓縮特性研究[J]．土木工程學報，

[4]王立忠，李玲玲．結構性軟土非線彈性模型中泊松比的取值[J]．水利學報，2006，37(2)：150—159

(本文來源：陜西省土木建筑學會  文徑網絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)

上一篇： 住房價格統計中的樣本代表性誤差及其修正

下一篇： 橋梁墩柱基于性能的抗震設計方法