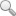陜西土木建筑網首頁 > 學術研究 > 課題研究 > 環形張拉整體結構的研究和應用

摘要：通過在索穹頂結構中引入環形張拉整體圈梁，提出一種新型索穹頂，并對初始預應力分布和結構性能進行了分析。算例結果表明該新型索穹頂是一種剛度較好且完全自支承自平衡的張拉整體結構。此研究豐富了現有張拉整體結構形式及其應用。...

環形張拉整體結構的研究和應用

袁行飛  彭張立  董石麟

浙江大學空間結構研究中心，浙江杭州  310027

引言

    張拉整體結構(Tensegrity)是一種由連續拉索和斷續壓桿構成的新型空間結構，最先由美國建筑師 FuⅡer…提出。自Snelson在1948年制作了第一個張拉整體模型以來，在過去的60年里，學者們對各種不同的張拉整體結構進行了廣泛研究，如正圓柱形張拉整體結構和球形張拉整體結構。但是作為另一種基本的幾何拓撲形態——環形張拉整體結構卻很少受到學者和工程師們的關注。

    本文提出了一種新型環形張拉整體結構，并對其拓撲和找形進行了研究，采用平衡矩陣方法求解了環形張拉整體結構的自應力模態和機構位移模態。通過在索穹頂中引入張拉整體環梁，提出了一種完全張拉整體式、且自支承自平衡的新型索穹頂體系。結構分析表明該體系具有較好的剛度，可用于實際工程。本文的研究在拓寬現有張拉整體結構形式及其應用方面進行了探索。

1、環形張拉整體結構的拓撲

    環形張拉整體結構的拓撲可通過在環向組合張拉整體棱柱得到。如組成單體數目為n，每個單體中壓桿數目為m，則該環形張拉整體結構可標記為 T(m—n)，T為Torus的首字母。

    圖1簡單地給出了T(4—3)型環形張拉整體模型的形成過程。圖中粗線代表壓桿，細線代表索，虛線代表附加索。

 

2、環形張拉整體結構的找形分析

    環形張拉整體結構的找形分析過程可歸納如下：

    (1)給定初始扭轉角θ，建立平衡矩陣A。

    (2)通過對平衡矩陣進行奇異值分解獲得自應力模態和機構位移模態[6]。

    (3)判斷是否存在桿受壓、索受拉的可行預應力模態。如果可行預應力模態不存在，重新設定扭轉角0進行計算。

 

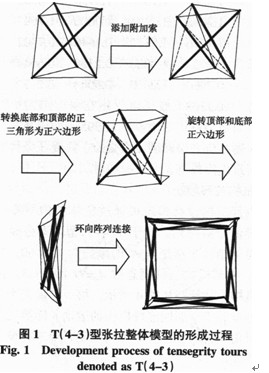
    (4)如果存在合理的可行預應力模態，則進一步分析環形張拉整體結構的幾何穩定性。幾何穩定性的分析可以參考Pellegfin0提出的幾何力方法。下面以T(4—    (3)型環形張拉整體結構為例，進行結構找形分析。圖3為T(4—3)型環形張拉整體結構的連接圖。在該結構中，節點總數為24，總自由度為72，單元總數為60，其中有12根壓桿、24根鞍索、l2根垂直索和12根附加索。Mx=6-mn<0。表明此結構是一個欠約束的結構，即一動不定的結構，而非通常的靜定或超靜定結構。

    由于環向對稱性，取兩個相鄰的單體進行找形分析。設圓環外圈半徑和內圈半徑的平均值為Rt，環形張拉整體中各個正多邊形截面的外接圓半徑為r，扭轉角為0，單體相對的圓心角χ=2π/n。

    2.1節點坐標

    2.2自應力模態

    單體有36個單元，編號為1-30和37～42。兩個單體的平衡矩陣A為36×36。當θ=π/3時，可得矩陣A的秩為34，存在兩個獨立的自應力模態t1和ι20通過組合兩個獨立的自應力模態。

    上述自應力模態滿足索受拉、桿受壓條件，是一種可行自應力模態。

    2.3機構位移模態

    內部機構位移模態可通過整體結構平衡矩陣A。的奇異值分解得到。對于T(4—3)型環形張拉整體結構，總體結構平衡矩陣At的維數為72×60，它的秩為58。內部機構位移模態數din=72—58—6=8。第一種模態為沿水平方向的類似于平面四連桿機構的運動，而第二種模態為以對角線為軸線的豎向機構運動，第三種模態為單體的擴展。

3、環形張拉整體結構作環梁的新型索穹頂結構

    索穹頂結構是由拉索和壓桿組成的自應力空間結構體系，最早由GeigerC[7]提出并應用在漢城奧運會的體操館和擊劍館。由于該結構體系具有受力合理、自重輕、跨度大、形式美觀、結構效率高等特點，索穹頂結構成為國內外學術界、工程界關注的熱點。現有的索穹頂結構大多支承于鋼筋混凝土圈梁或環形鋼桁架，所以從嚴格意義上說不屬于張拉整體的范疇。如果把環形張拉整體結構作為環梁引入索穹頂結構，則可以得到如圖5所示的真正意義上的張拉整體索穹頂結構。

    布置三道環索，環向十二等分，外徑50m的新型Levy型索穹頂。索穹頂中壓桿和索截面面積分別為0.05㎡和0.001㎡。張拉整體環梁為12等分，內徑42m，外徑58m，截面正多邊形外接圓的半徑為4m。環梁中壓桿和索的截面面積分別為0.1㎡和0.01㎡。壓桿和索的屈服應力分別為345MPa和1860MPa，楊氏模量分別為2×1011N/m2和1.85×1011N/㎡。為保證一定的安全度，整個體系中索的最大允許預應力為639MPa。

    對于這兩組自應力模態，可以根據索穹頂和環形張拉整體中索的最大容許應力給出所有構件的初始應力，其中1～30組代表環形張拉整體結構的預應力，31～43組代表索穹頂的預應力。

    非線性計算后最大的位移為0.02186m。如不修正幾何形狀，直接將第一次協同找形得到的內力作為初始預應力模態進行迭代計算，可得最大的位移為0.001308m，此時環梁中索內力和索穹頂中索內力相差較大。如果繼續迭代，會發現索穹頂中預應力將逐漸趨向于零。因為環形張拉整體結構是一個完全自平衡的體系，只有索穹頂中桿件內力為零時，與環梁連接節點處合力才為零。顯然這種預應力分布在實際工程中是不可行的。

    因此本文以第一次協同找形后得到的預應力分布和幾何外形作為新型索穹頂的初始預應力分布和外形，進行結構性能分析。

    新型索穹頂結構作用豎向均布荷載0.5kN/㎡。張拉整體環底部節點豎向約束。采用ANSYS對新型索穹頂模態進行分析，發現環形張拉整體結構作為環梁的新型索穹頂結構頻率比較密集。從第l階模態到第13階模態都是索穹頂內環索桿局部振動，而從第14階模態(f=3.41 Hz)開始，新型體系的振型轉變成整體的振動，說明該結構體系剛度較好。

4、結論

    本文提出了一種新型環形張拉整體結構，并對其拓撲和找形問題進行了詳細的分析，根據平衡矩陣理論，得出了環形張拉整體結構的自應力模態和機構位移模態。

    作為張拉整體結構的應用，提出了一種以環形張拉整體結構作為環梁的新型索穹頂體系，經機構判定為一可行體系，是真正意義上自平衡自支承的張拉整體結構。采用非線性有限元方法對整體結構進行協同找形，確定結構初始預應力和外形，并進行了結構靜、動力性能分析，算例結果表明該結構具有較好的剛度，能應用于實際工程。

(本文來源：陜西省土木建筑學會  文徑網絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)

上一篇： 混凝土樓地板輻射采暖的質量控制

下一篇： 含有機質粉質粘土的壓縮試驗與性狀分析